Exercice corrigé - Polynômes du second et troisième degré - Factorisation, racines et étude du signe
Factorisation, racines et signe
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Factorisation d'un polynômes du troisième degré, recherche de ses racines, et détermination de son signe
Exercice - énoncé:
On considère le polynôme
 .
.
Cacher la correction
- Montrer que
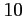 est une racine de
est une racine de 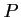 .
.
- En déduire une factorisation du polynôme
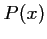 .
.
- Déterminer alors toutes les solutions de l'équation
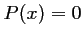 .
.
- Déterminer les valeurs de
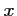 pour lesquelles
pour lesquelles 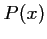 est positif
ou nul.
est positif
ou nul.
Correction exercice
-
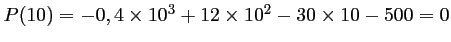 .
.
On én déduit que
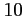 est bien une racine du polynôme
est bien une racine du polynôme 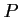 .
.
- D'après la question précédente, on sait que le polynôme
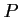 se
factorise suivant:
se
factorise suivant:
 , où
, où 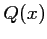 est un polynôme de degré 2:
est un polynôme de degré 2:
 .
.
On a donc,
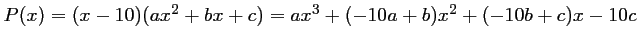 , d'où on déduit que
, d'où on déduit que
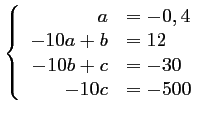 ,
soit donc,
,
soit donc,
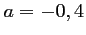 ,
, 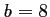 et
et 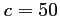 .
.
On trouve donc la factorisation:
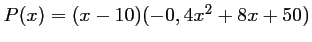 .
.
-
 ,
et donc, soit
,
et donc, soit
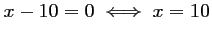 ,
soit
,
soit
 :
:
 .
Le trinôme admet donc deux solutions:
.
Le trinôme admet donc deux solutions:
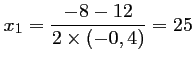 et
et
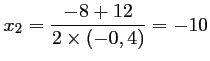 .
.
Ainsi l'ensemble des solutions est
 .
.
- On cherche les valeurs de
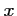 pour lesquelles
pour lesquelles
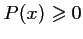 ,
soit aussi,
,
soit aussi,
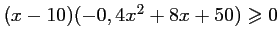 :
:
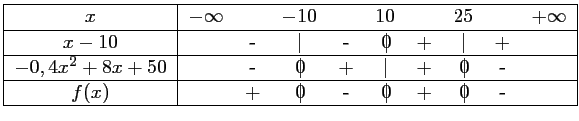
On a alors, ![$ P(x)\geqslant0 \Longleftrightarrow
x\in]-\infty;-10]\cup[10;25]$](/Generateur-Devoirs/1S/Chap1/ex9_c_img24.png) .
.
Cacher la correction
Voir aussi: