Exercice corrigé - Second degré: Intersection de deux paraboles
Intersection d'une parabole et d'une droite
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé sur Second degré - Recherche de l'intersection de deux paraboles définies avec un paramètre
Exercice - énoncé:
On considère les fonctions 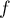 et
et 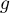 définies sur
définies sur 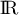 par
les expressions
par
les expressions  et
et 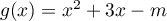 ,
où
,
où 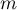 est un nombre réel.
est un nombre réel.
Déterminer les éventuelles valeurs de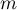 pour lesquelles
les courbes
pour lesquelles
les courbes 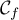 et
et  ,
représentatives des fonctions
,
représentatives des fonctions 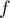 et
et  ,
ont un unique point d'intersection.
,
ont un unique point d'intersection.
Donner alors les coordonnées de ce point d'intersection.
Si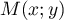 est un éventuel point d'intersection,
alors
est un éventuel point d'intersection,
alors 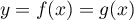 , soit donc l'équation
, soit donc l'équation
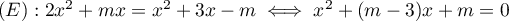 .
.
Le discriminant de cette équation du second degré est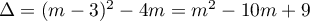 .
.
On veut que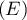 ait une unique solution,
donc que
ait une unique solution,
donc que 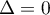 .
.
 est expression du second degré de discriminant
est expression du second degré de discriminant
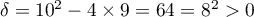 et admet donc deux racines
et admet donc deux racines
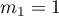 et
et 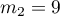 .
.
Pour ,
, 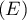 s'écrit
s'écrit 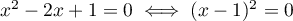 .
Ainsi
.
Ainsi  et
et 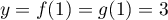 et
et 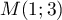 est l'unique point d'intersection.
est l'unique point d'intersection.
Pour ,
, 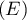 s'écrit
s'écrit 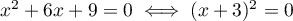 .
Ainsi
.
Ainsi  et
et 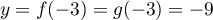 et
et 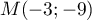 est l'unique point d'intersection.
est l'unique point d'intersection.
Cacher la correction
Déterminer les éventuelles valeurs de
Donner alors les coordonnées de ce point d'intersection.
Correction exercice
Si
Le discriminant de cette équation du second degré est
On veut que
Pour
Pour
Cacher la correction
Voir aussi: