Exercice corrigé - Courbe d'un tobogan
Ajustement d'une courbe à partir de ses tangentes
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Modélisation d'un tobogan: ajustement d'une courbe avec ses tangentes
Exercice - énoncé:
Pour faire franchir à des chariots une marche de deux mètres de haut,
sur une distance de horzontale de cinq mètres, on cherche à construire
un tobogan.
![\begin{pspicture}(-1,-1)(6,3)
\psline[arrowsize=5pt,linewidth=0.4pt]{->}(-2.5,0...
...$}
\rput(-0.3,2){$2$}
\rput(-0.2,-0.2){$O$}
\rput(5,2.3){$A$}
\end{pspicture}](/Generateur-Devoirs/1S/Chap3/ex6_img6.png)
Cacher la correction
Dans un repère
![]() la courbe
la courbe
![]() , qui est une vue en coupe du tobogan, doit
obéir aux contraintes suivantes:
, qui est une vue en coupe du tobogan, doit
obéir aux contraintes suivantes:
- la courbe passe par les points
 et
et 
- les tangentes en
 et
et 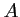 sont horizontales
(pour se raccorder sans "angle" avec le sol).
sont horizontales
(pour se raccorder sans "angle" avec le sol).
![\begin{pspicture}(-1,-1)(6,3)
\psline[arrowsize=5pt,linewidth=0.4pt]{->}(-2.5,0...
...$}
\rput(-0.3,2){$2$}
\rput(-0.2,-0.2){$O$}
\rput(5,2.3){$A$}
\end{pspicture}](/Generateur-Devoirs/1S/Chap3/ex6_img6.png)
- On recherche une fonction polynôme du troisième degré:
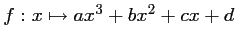 , et dont la courbe
représentative est
, et dont la courbe
représentative est
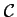 .
.
Déterminer les coefficients
 ,
, 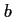 ,
, 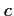 et
et 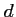 pour que la courbe
pour que la courbe
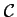 représentative de
représentative de 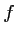 convienne.
convienne.
- Déterminer les coordonnées du point
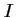 milieu de
milieu de ![$ [OA]$](/Generateur-Devoirs/1S/Chap3/ex6_img14.png) .
Ce point appartient-il à
.
Ce point appartient-il à
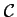 ?
?
La pente en un point de la courbe est le coefficient directeur de la tangente à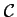 en ce point.
en ce point.
Quelle est la pente de
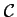 en
en 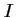 ?
?
Correction exercice
- La fonction
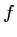 doit vérifier les conditions suivantes:
doit vérifier les conditions suivantes:

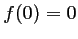 soit, comme
soit, comme 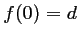 ,
, 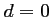 .
.

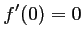 soit, comme
soit, comme
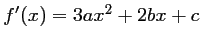 , donc
, donc 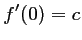 , et
, et 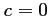 .
.
On a alors,
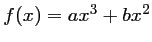 .
.

-
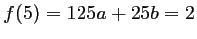

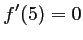 soit, comme
soit, comme
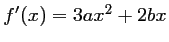 ,
l'équation
,
l'équation 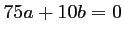
Les deux dernières équations permettent de calculer
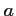 et
et 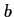 :
:
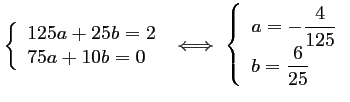
En résumé, la fonction
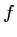 s'écrit
s'écrit
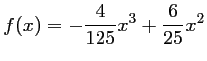 .
.
- Le point
 , milieu de
, milieu de ![$ [OA]$](/Generateur-Devoirs/1S/Chap3/ex6_c_img20.png) a pour coordonnées
a pour coordonnées
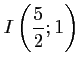 .
.
De plus,
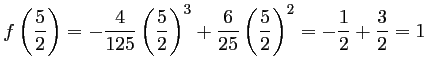 .
.
Ainsi, le point
 appartient à
appartient à
 .
.
La pente en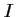 est
est
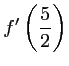 ,
or
,
or
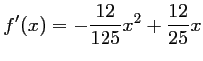 ,
et donc,
,
et donc,
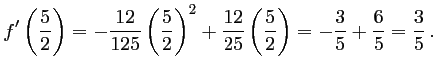
La pente en
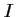 est donc de
est donc de
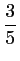 .
.
Cacher la correction
Voir aussi: