Exercice corrigé - Etude d'une fonction avec paramètres
Ajustement de paramètres et étude de fonction
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Dérivée d'une fonction avec paramètres à déterminer, étude du sens de variation, tangente
Exercice - énoncé:
On appelle 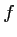 la fonction définie sur
la fonction définie sur
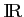 par
par
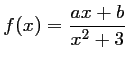 ,
,
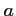 et
et 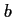 désignant deux constantes réelles,
et
désignant deux constantes réelles,
et
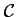 la courbe de
la courbe de 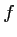 .
.
On appelle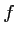 la fonction définie sur
la fonction définie sur
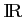 par
par
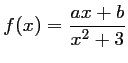 ,
,
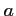 et
et 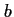 désignant deux constantes réelles,
et
désignant deux constantes réelles,
et
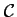 la courbe de
la courbe de 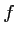 .
.
Cacher la correction
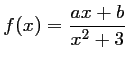 ,
,
- Démontrer que la dérivée de
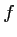 s'écrit
s'écrit
 .
.
- Déterminer les valeurs de
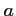 et
et 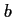 pour que
pour que
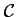 passe
par le point
passe
par le point 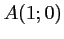 et admette en ce point une tangente de
coefficient directeur
et admette en ce point une tangente de
coefficient directeur
 .
.
Dans toute la suite, on prendra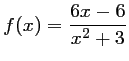 .
.
- Etudier les variations de
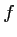 , et dresser son tableau de
variation.
, et dresser son tableau de
variation.
- Donner une équation de la tangente
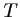 à la courbe de
à la courbe de 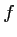 en
en
 .
.
- Tracer
 et
et
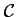 dans le plan muni d'un repère
orthogonal d'unité 1 cm en abscisse et 3 cm en ordonnée.
dans le plan muni d'un repère
orthogonal d'unité 1 cm en abscisse et 3 cm en ordonnée.
Correction exercice
On appelle
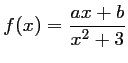 ,
,
- On a
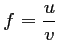 ,
avec
,
avec 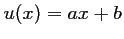 ,
, 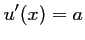 et
et
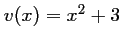 ,
, 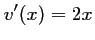 ,
et donc,
,
et donc,
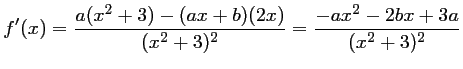
- On veut que
 passe par
passe par 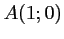 ,
c'est-à-dire que
,
c'est-à-dire que
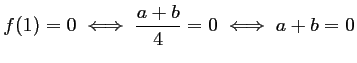 .
.
De plus, le coefficient directeur de la tangente en
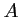 est
est
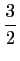 , c'est-à-dire
, c'est-à-dire
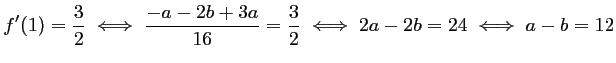
En résumé, on doit avoir
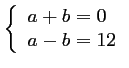 .
.
En ajoutant et soustrayant ces deux équations, on trouve
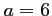 et
et 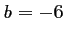 , soit
, soit
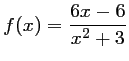 .
.
- D'après 1., on a
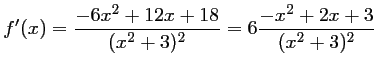 .
.
Le trinôme du second degré au numérateur a pour racines
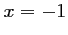 et
et 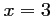 , et on a alors:
, et on a alors:
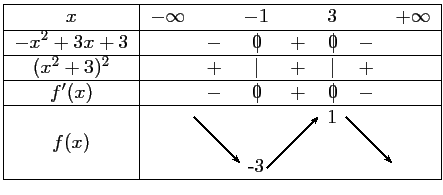
- En
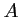 , on a
, on a
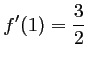 , et
, et 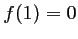 ,
d'où l'équation de la tangente
,
d'où l'équation de la tangente  à la courbe de
à la courbe de 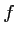 en
en
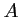 :
:
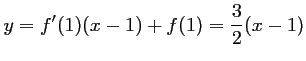
-
![\begin{pspicture}(-5,-3.5)(5,2)
\psline[arrowsize=6pt]{->}(-5,0)(5,0)
\psline[...
...3){$A$}
\psplot{-0.7}{2.3}{1.5 x 1 sub mul}
\rput(2,1.8){$T$}
\end{pspicture}](/Generateur-Devoirs/1S/Chap3/ex2_c_img30.png)
Cacher la correction
Voir aussi: