Exercice corrigé - Etude d'une fonction à l'aide d'une fonction auxiliaire
Etude à l'aide d'une fonction auxiliaire
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Etudes de fonctions, à l'aide d'une fonction auxiliaire et du théorème des valeurs intermédiaires
Exercice - énoncé:
Partie A.
Soit ![]() la fonction définie sur
la fonction définie sur
![]() par
par
![]() .
.
- Etudier le sens de variation de
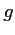 .
.
- En déduire que l'équation
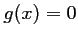 admet une seule solution sur
admet une seule solution sur
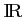 et que cette solution, notée
et que cette solution, notée 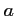 , est comprise entre
, est comprise entre 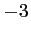 et
et
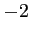 .
.
- Etudier le signe de
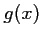 pour
pour
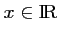 .
.
Partie B.
Soit ![]() la fonction définie sur
la fonction définie sur
![]() par
par
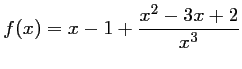 .
.
Montrer que pour tout réel non nul ![]() ,
,
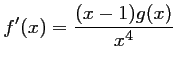 , et en déduire les variations de
, et en déduire les variations de ![]() .
.
Correction exercice
Partie A.
Soit ![]() la fonction définie sur
la fonction définie sur
![]() par
par
![]() .
.
- Pour tout
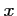 réel,
réel,
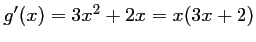 .
.
![$\displaystyle \begin{tabular}[t]{\vert c\vert ccccccc\vert}\hline
$x$& $-\inft...
...row$}
& & \Large {$\nearrow$} &\\
& & & & &$6$\ & &\\ \hline
\end{tabular}$](/Generateur-Devoirs/1S/Chap3/ex10_c_img6.png)
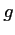 est dérivable sur
est dérivable sur ![$ [-3;2]$](/Generateur-Devoirs/1S/Chap3/ex10_c_img7.png) , et est
strictement croissante.
On a de plus,
, et est
strictement croissante.
On a de plus,
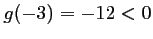 et
et 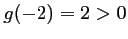 .
On en déduit donc, d'après le théorème des valeurs intermédiaires,
que l'équation
.
On en déduit donc, d'après le théorème des valeurs intermédiaires,
que l'équation 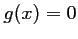 admet une unique solution sur
admet une unique solution sur ![$ [-3;2]$](/Generateur-Devoirs/1S/Chap3/ex10_c_img7.png) .
.
De plus, d'après le tableau de variation de
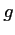 ,
pour
,
pour 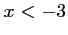 , on a
, on a
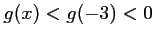 et pour tout
et pour tout 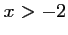 ,
, 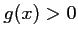 .
Ainsi, il n'y a pas d'autre solution à l'équation
.
Ainsi, il n'y a pas d'autre solution à l'équation 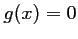 en dehors
de l'intervalle
en dehors
de l'intervalle ![$ [-3;-2]$](/Generateur-Devoirs/1S/Chap3/ex10_c_img15.png) , et
l'équation
, et
l'équation 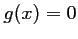 admet donc une unique solution sur
admet donc une unique solution sur
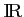 qui est
comprise entre
qui est
comprise entre 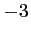 et
et 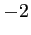 .
.
- D'après ce qui précède, on a:
![$\displaystyle \begin{tabular}[t]{\vert c\vert ccccc\vert}\hline
$x$& $-\infty$...
...(x)$\ & & $-$\ & \mbox{$0\hspace{-0.67em}\mid$}& $+$\ &\\ \hline
\end{tabular}$](/Generateur-Devoirs/1S/Chap3/ex10_c_img18.png)
Partie B.
Soit ![]() la fonction définie sur
la fonction définie sur
![]() par
par
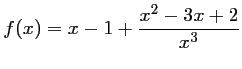 .
.
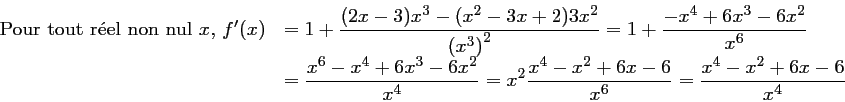
Or,
ce qui montre que l'on a bien
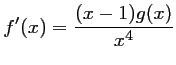 .
.
A l'aide de la partie A, on en déduit alors:
![$\displaystyle \begin{tabular}[t]{\vert c\vert ccccccccc\vert}\hline
$x$& $-\inf...
...Large {$\searrow$}&&\Large {$\nearrow$}& \\
&&&&&&&0&& \\ \hline
\end{tabular}$](/Generateur-Devoirs/1S/Chap3/ex10_c_img25.png)
Cacher la correction
Voir aussi: