Exercice corrigé - ROC: dérivation et inégalités
ROC et Application
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - ROC: dérivée d'inégalités
Exercice - énoncé:
- Soit
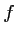 et
et 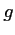 deux fonctions dérivables sur
deux fonctions dérivables sur ![$ I=[0;1]$](/Generateur-Devoirs/1S/Chap3/ex13_img3.png) telles que
telles que
 et pour tout
et pour tout ![$ x\in[0;1]$](/Generateur-Devoirs/1S/Chap3/ex13_img5.png) ,
,
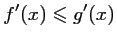 .
.
Démontrer que pour tout ,
,
 .
.
(Indication: on pourra étudier les variations de la fonction
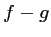 .)
.)
- Application.
Soit les fonctions
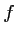 et
et 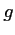 définies sur
définies sur ![$ I=[0;1]$](/Generateur-Devoirs/1S/Chap3/ex13_img3.png) par
par
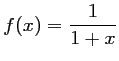 et
et
 .
.
Montrer que pour tout
![$ x\in[0;1]$](/Generateur-Devoirs/1S/Chap3/ex13_img5.png) ,
,
 .
.
Correction exercice
- Soit la fonction
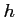 définie sur
définie sur 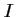 par
par
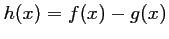 .
.
Alors, pour tout
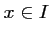 ,
,
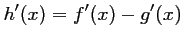 ,
et donc, comme
,
et donc, comme
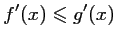 ,
pour tout
,
pour tout 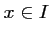 ,
,
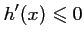 .
.
On en déduit que la fonction
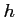 est décroissante sur
est décroissante sur 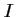 .
.
On sait de plus que
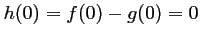 , et donc le tableau de
variation de
, et donc le tableau de
variation de  :
:
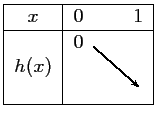
On en déduit en particulier que pour tout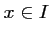 ,
,
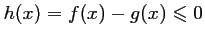 ,
c'est-à-dire que
,
c'est-à-dire que
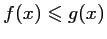 .
.
- Soit
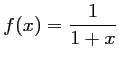 et
et
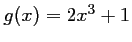 .
On a
.
On a
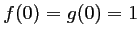 .
.
De plus, pour tout
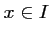 ,
,
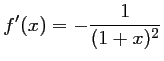 et
et
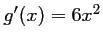 ,
d'où,
,
d'où,
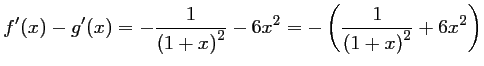
Or, pour tout![$ x\in[0;1]$](/Generateur-Devoirs/1S/Chap3/ex13_c_img18.png) ,
,
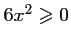 et
et
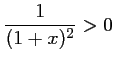 .
On a donc, pour tout
.
On a donc, pour tout 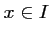 ,
,
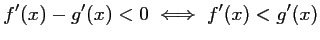 .
.
On en déduit donc, d'après la question 1., que pour tout
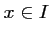 ,
,
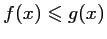 .
.
Cacher la correction
Voir aussi: