Exercices 3: Etude d'une fonction rationnelle
Dérivée d'une fonction, détermination du sens de variation
Exercice 3
Exercice 3
On considère la fonction
définie par l'expression
.
On note
sa courbe représentative.
- Dresser le tableau de variation de
.
- Tracer l'allure de la courbe
.
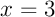
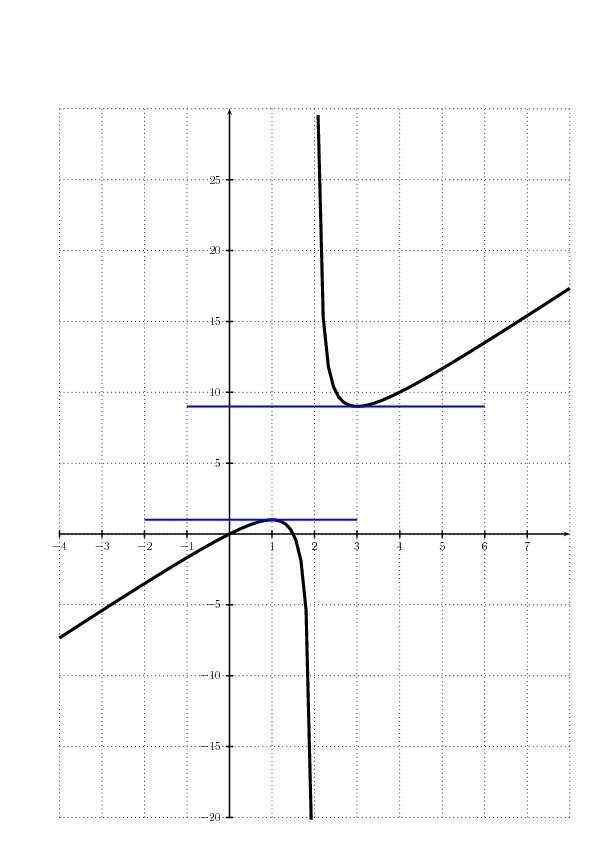
Exercice 3