Exercice 2: Etude d'une fonction polynomiale du 3ème degré
Dérivée d'une fonction - Equation de tangentes
Exercice 2
Exercice 2: dérivée et variation d'un polynôme de degré 3
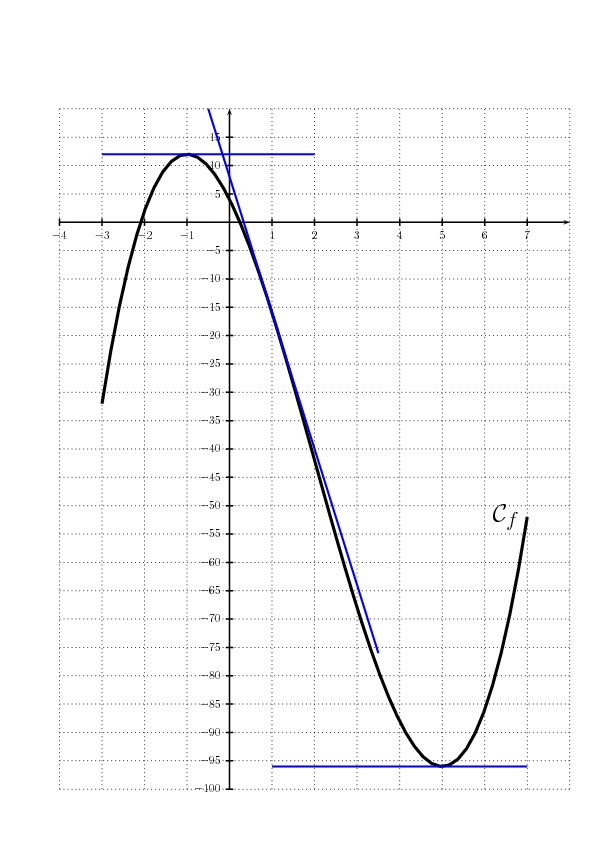
On considère la fonction f (x) = x3 − 6x2 − 15x + 4 définie sur l'intervalle [ −3 ; 7]On note Cf sa courbe représentative.
- Dresser le tableau de variation de f.
C'est le signe de la dérivée de la fonction qui nous donne son sens de variation.
La dérivée de f est f' (x) = 3x2 − 12x −15 soit aussi, en factorisant f' (x) = 3(x2 − 4x −5)
Le trinôme du second degré a pour discriminant Δ=(−4)2−4×1×(−5)=36>0 et admet donc 2 racines: x1 = −(−4) − 362×1 = −1 et de même x2 = −(−4) + 362×1 = 5
x −3 −1 5 7 f' (x) + 0 − 0 + 12 −52 f ↗ ↘ ↗ −32 −96
- Déterminer l'équation de la tangente à Cf au point d'abscisse x = 1.
L'équation générale de la tangente en est :
est :
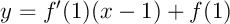
On calcule alors: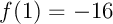 et
et
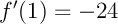
d'où l'équation de la tangente:
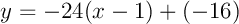 ou encore
ou encore
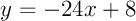
- Tracer cette tangente et la courbe Cf
Exercice 2