Série entière presque géométrique
Colle de mathématiques
Sujet de colle de maths:- Séries entièresSéries entières
Énoncé du sujet
Donner le rayon de convergence et donner une expression à l'aide de fonctions usuelles de la série
 .
.
 .
.
Correction
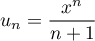 est le terme général de la série,
on a
est le terme général de la série,
on a  lorsque
lorsque  .
.
Le rayon de convergence de cette série entière est donc 1, et on suppose donc dans les tous les calculs à venir que .
.
Soit donc, pour ,
, 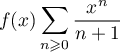 .
.
et, .
.
On a alors, la série entière étant dérivable, et terme à terme, dans son disque de convergence,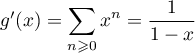 .
.
On trouve alors en intégrant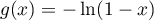 d'où
d'où
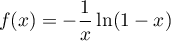 .
.
Remarque: on peut vérifier (question supplémentaire ?) pour la seule valeur facilement calculable de la série: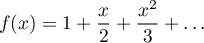 donc
donc 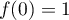 .
.
Avec le résultat trouvé, comme en 0,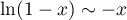 , on a bien
en prolongeant par continuité en 0 l'expression trouvée
, on a bien
en prolongeant par continuité en 0 l'expression trouvée
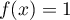 .
.
Correction
SiLe rayon de convergence de cette série entière est donc 1, et on suppose donc dans les tous les calculs à venir que
Soit donc, pour
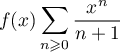 .
.
et,
 .
.
On a alors, la série entière étant dérivable, et terme à terme, dans son disque de convergence,
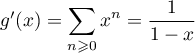 .
.
On trouve alors en intégrant
Remarque: on peut vérifier (question supplémentaire ?) pour la seule valeur facilement calculable de la série:
Avec le résultat trouvé, comme en 0,
Tag:Séries entières
Autres sujets au hasard:
