Formule de Bayes
Colle de mathématiques
Sujet de colle de maths:- Probabilités conditionnelles - indépendanceProbabilités conditionnelles - indépendance
Énoncé du sujet
- Démontrer la formule de Bayes: pour deux événements
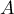 et
et 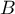 de probabilités non nulles,
de probabilités non nulles,
![\[P_B(A)=P_A(B)\dfrac{P(A)}{P(A)\times P_A(B)+P\lp\overline{A}\rp\times P_{\overline{A}}(B)}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours3/3.png)
- J'ai trois pièces dans ma poche, deux normales, et une avec "Pile" sur ses deux faces.
Je prends une pièce au hasard dans ma poche, la lance et obtiens "Pile".
Quelle est la probabilité que cette pièce présente aussi "Pile" sur son autre face ?
Correction
Correction
- On a tout d'abord la définition d'une probabilité conditionnelle:
![\[P_B(A)=\dfrac{P\left( A\cap B\right)}{P(B)}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours3_c/1.png)
et inversement
![\[P_A(B)=\dfrac{P\left( A\cap B\right)}{P(A)}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours3_c/2.png)
ansi,
![\[P\left( A\cap B\rp=P_A(B)\times P(A)=P_B(A)\times P(B)\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours3_c/3.png)
d'où
![\[P_B(A)=P_A(B)\dfrac{P(A)}{P(B)}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours3_c/4.png)
De plus, comme
![\[B=\left( B\cap A\rp\cup\left( B\cap \overline{A}\rp\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours3_c/5.png)
et comme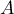 et
et 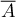 sont disjoints, donc
sont disjoints, donc
 et
et  aussi
aussi
![\[\begin{array}{ll}P(B)&=P\left( B\cap A\right) + P\left( B\cap \overline{A}\right)\\[.7em]
&=P(A)\times P_A(B)+P\lp\overline{A}\rp\times P_{\overline{A}}(B)\enar\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours3_c/10.png)
qui est la formule des probabilités totales.
On obtient donc
![\[P_B(A)=P_A(B)\dfrac{P(A)}{P(A)\times P_A(B)+P\lp\overline{A}\rp\times P_{\overline{A}}(B)}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours3_c/11.png)
- On note les événements:
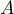 : "la pièce prise dans ma poche est la pièce avec Pile sur les deux faces"
et
: "la pièce prise dans ma poche est la pièce avec Pile sur les deux faces"
et  : "j'obtiens Pile", et on cherche donc la probabilité
: "j'obtiens Pile", et on cherche donc la probabilité
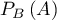 .
.
On a alors, d'après l'énoncé,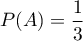 ,
, 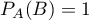 et, pour les pièces normales (équilibrées)
et, pour les pièces normales (équilibrées)
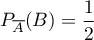 ,
,
La formule de Bayes de la question précédente s'écrit ici
![\[\begin{array}{ll}P_B(A)&=P_A(B)\dfrac{P(A)}{P(A)\times P_A(B)+P\lp\overline{A}\rp\times P_{\overline{A}}(B)}\\[.8em]
&=1\tm\dfrac{\frac13}{\frac13\tm1+\frac23\tm\frac12}\\[.8em]
&=\dfrac{1}{2}
\enar\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours3_c/18.png)
Tag:Probabilités conditionnelles - indépendance
Autres sujets au hasard:

Voir aussi: