Polynôme définissant par une relation avec sa dérivée
Colle de mathématiques
Sujet de colle de maths:- PolynômePolynômes
Énoncé du sujet
Soit ![$P\in\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP5/1.png) un polynôme non nul qui vérifie
un polynôme non nul qui vérifie
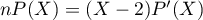 .
.
- Déterminer le degré de
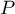 . En déduire que
. En déduire que 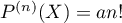 ,
avec
,
avec  .
.
- Montrer, par récurrence sur
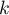 , que, pour tout entier
, que, pour tout entier 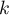 ,
,
![\[P^{(k)}(X)=\dfrac1n\Bigl((X-2)P^{(k+1)}(X)+kP^{(k)}(X)\Bigr)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP5/8.png)
- Montrer que
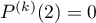 pour
pour 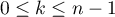 .
.
- En déduire
 en fonction de
en fonction de  et
et 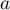 .
.
Correction
Correction
- Soit
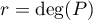 , c'est-à-dire que
, c'est-à-dire que
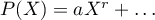 avec
avec 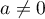 .
.
On a alors
![\[\begin{array}{ll}&nP(X)=naX^r+\dots\\
&=(X-2)\left( arX^{r-1}+\dots\rp=arX^r+\dots
\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP5_c/4.png)
ce qui montre que, nécessairement, .
.
On a alors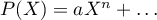 , puis en dérivant
, puis en dérivant 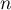 fois
fois
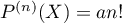 .
.
- Pour
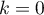 , la relation s'écrit
, la relation s'écrit
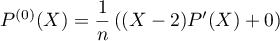 qui la relation définissant
qui la relation définissant 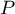 .
.
Supposant maintenant que pour un entier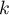 on ait
on ait
![\[P^{(k)}(X)=\dfrac1n\Bigl((X-2)P^{(k+1)}(X)+kP^{(k)}(X)\Bigr)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP5_c/13.png)
alors,
![\[\begin{array}{ll}P^{(k+1)}(X)&=\left( P^{(k)}\rp'(X)\\[.8em]
&=\dfrac1n\biggl(P^{(k+1)}(X)+(X-2)P^{(k+2)}(X)+kP^{(k+1)}(X)\biggr)\\[1em]
&=\dfrac1n\biggl((X-2)P^{(k+2)}(X)+(k+1)P^{(k+1)}(X)\biggr)
\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP5_c/14.png)
qui montre que la relation est encore vraie au rang suivant, et donc que, d'après le principe de récurrence, cette relation est vraie pour tout entier .
.
- La relation précédente, pour
 donne
donne
![\[P^{(k)}(2)=\dfrac1n\biggl(0+kP^{(k)}(2)\biggr)
\iff (n-k)P^{(k)}(2)=0\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP5_c/17.png)
et donc que, pour tout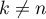 , on a
, on a 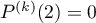 .
.
- Le résultat précédent montre que 2 est une racine de multiplicité
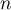 et donc que
et donc que
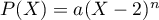 .
.
Tag:Polynôme
Autres sujets au hasard:

Voir aussi: