Inverse d'une matrice 2x2 par le pivot de Gauss-Jordan
Colle de mathématiques
Sujet de colle de maths:- MatricesMatrices
Énoncé du sujet
En utilisant l'algorithme du pivot de Gauss-Jordan, calculer l'inverse
de la matrice
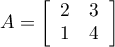 .
.
Correction
![\[\lb\begin{array}{rr|rr}2&3 &1&0\\1&4 &0&1\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/1.png)
On ramène le pivot de la 1ère ligne à 1 par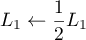 ,
,
![\[\lb\begin{array}{rr|rr}1&\dfrac32 &\dfrac12&0\\1&4 &0&1\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/3.png)
puis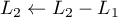
![\[\lb\begin{array}{rr|rr}1&\dfrac32 &\dfrac12&0\\[.8em]0&\dfrac52 &-\dfrac12&1\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/5.png)
puis on ramène à 1 le pivot de la 2ème ligne par
![\[\lb\begin{array}{rr|rr}1&\dfrac32 &\dfrac12&0\\[.8em]0&1 &-\dfrac15&\dfrac25\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/7.png)
puis enfin on calcule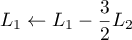
![\[\lb\begin{array}{rr|rr}1&0 &\dfrac45&\dfrac35\\[.8em]0&1 &-\dfrac15&\dfrac25\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/9.png)
d'où on trouve
![\[A^{-1}=\lb\begin{array}{rr}\dfrac45&\dfrac35\\[.8em]-\dfrac15&\dfrac25\enar\right]
=\dfrac15\lb\begin{array}{rr}4&3\\[.8em]-1&2\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/10.png)
Correction
On écrit la matrice augmentée avec l'identitéOn ramène le pivot de la 1ère ligne à 1 par
![\[\lb\begin{array}{rr|rr}1&\dfrac32 &\dfrac12&0\\1&4 &0&1\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/3.png)
puis
![\[\lb\begin{array}{rr|rr}1&\dfrac32 &\dfrac12&0\\[.8em]0&\dfrac52 &-\dfrac12&1\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/5.png)
puis on ramène à 1 le pivot de la 2ème ligne par
![\[\lb\begin{array}{rr|rr}1&\dfrac32 &\dfrac12&0\\[.8em]0&1 &-\dfrac15&\dfrac25\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/7.png)
puis enfin on calcule
![\[\lb\begin{array}{rr|rr}1&0 &\dfrac45&\dfrac35\\[.8em]0&1 &-\dfrac15&\dfrac25\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/9.png)
d'où on trouve
![\[A^{-1}=\lb\begin{array}{rr}\dfrac45&\dfrac35\\[.8em]-\dfrac15&\dfrac25\enar\right]
=\dfrac15\lb\begin{array}{rr}4&3\\[.8em]-1&2\enar\rb\]](/Generateur-Devoirs/Colles/matrices/inverse-GJ_c/10.png)
Tag:Matrices
Autres sujets au hasard:
