Développement en série entière d'une fonction
Colle de mathématiques
Sujet de colle de maths:- Séries entièresSéries entières
Énoncé du sujet
Développer en série entière au voisinage de 0 la fonction  .
.
Préciser le rayon de convergence de la série entière obtenue.
Préciser le rayon de convergence de la série entière obtenue.
Correction
 et de remplacer
et de remplacer 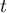 par
par 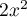 .
.
On a donc
![\[\ln(1+2x^2)=\sum_{n=1}^{+\infty}\frac{(-1)^{n+1}2^n x^{2n}}{n}\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE1_c/4.png)
La série converge si . Son rayon de convergence est donc
. Son rayon de convergence est donc 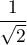 .
.
Correction
Il suffit d'écrire le développement en série entière deOn a donc
![\[\ln(1+2x^2)=\sum_{n=1}^{+\infty}\frac{(-1)^{n+1}2^n x^{2n}}{n}\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE1_c/4.png)
La série converge si
Tag:Séries entières
Autres sujets au hasard:
