Comportement asymptotique de l'espérance du max de lois exponentielles
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit 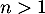 un entier et
un entier et 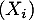 des variables aléatoires indépendantes de même loi exponentielle de paramètre 1.
On pose:
des variables aléatoires indépendantes de même loi exponentielle de paramètre 1.
On pose:
![\[M_n = \max\left( X_1 , \dots , X_n\rp\]](/Generateur-Devoirs/Colles/VAC/EmaxE/3.png)
- Montrer que
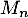 admet une densité, qu'on déterminera et qu'on représentera graphiquement.
admet une densité, qu'on déterminera et qu'on représentera graphiquement.
- Montrer que l’intégrale
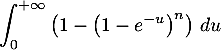 converge.
converge.
- Déterminer la valeur de la limite de
![$\dfrac{E\left[ M_n\right]}{\ln(n)}$](/Generateur-Devoirs/Colles/VAC/EmaxE/6.png) quand
quand 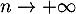 .
Indication : on pourra utiliser, sans preuve, le fait que
.
Indication : on pourra utiliser, sans preuve, le fait que
![$E[Y]=\dsp\int_0^{+\infty}P(Y\geqslant u)\,du$](/Generateur-Devoirs/Colles/VAC/EmaxE/8.png) pour toute variable aléatoire positive
pour toute variable aléatoire positive 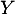 faire un changement de variable dans l’intégrale.
faire un changement de variable dans l’intégrale.
Correction
Correction
Oral ENS ULM - 2017- On a
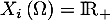 donc aussi
donc aussi 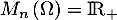 .
.
On note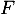 la fonction de répartition des
la fonction de répartition des 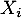 ,
donc
,
donc 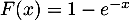 si
si 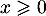 et 0 sinon, et on note de même
et 0 sinon, et on note de même 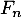 la fonction de répartition de
la fonction de répartition de 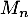 .
.
On a alors pour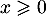 , et par indépendance des variables aléatoires,
, et par indépendance des variables aléatoires,
![\[\begin{array}{lcl}
F_n(x)&=&P\left( M_n\leqslant x\rp\\[.5em]
&=&P\left( \max(X_1,\dots,X_n)\leqslant x\rp\\[.5em]
&=&P\biggl( \left( X_1\leqslant x\rp\cap\dots\cap\left( X_1\leqslant x\rp\biggr)\\
&=&\dsp\prod_{i=1}^nP\left( X_i\leqslant x\rp\\[1.5em]
&=&\left( F(x)\rp^n
= \lp1-e^{-x}\rp^n\enar\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/10.png)
tandis que
![\[F_n(x)=P\left( M_n\leqslant x\rp=0 \text{ pour } x<0\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/11.png)
La fonction de densité est alors donnée par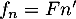 , soit
pour
, soit
pour 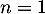 ,
,
![\[f_1(x)=\la\begin{array}{ll}0 &\text{ si } x<0\\e^{-x}&\text{ si } x\geqslant0\enar\right.\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/14.png)
et la courbe
(0,0)
\psplot[linecolor=blue,linewidth=1.5pt]{0}{5}{2.718 x -1 mul exp}
\psline(-.1,1)(.1,1)\rput[r](-.2,1){1}
\end{pspicture}\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/15.png)
Pour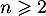 , on a
, on a
![\[f_n(x)=\la\begin{array}{ll}0 &\text{ si } x<0\\
ne^{-x}\lp1-e^{-x}\rp^{n-1}&\text{ si } x\geqslant0\enar\right.\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/17.png)
et donc, pour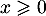 ,
,
![\[\begin{array}{lcl}
f_n'(x)&=&ne^{-x}\lp1-e^{-x}\rp^{n-2}\biggl(-\lp1-e^{-x}\rp+(n-1)e^{-x} \biggr)\\[1em]
&=&ne^{-x}\lp1-e^{-x}\rp^{n-2}\biggl(-1+ne^{-x}\biggr)
\enar\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/19.png)
et la fonction est donc croissante puis décroissante, avec un maximum en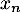 tel que
tel que
![\[-1+ne^{-x}=0 \iff x=\ln(n)\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/21.png)
et on obtient l'allure de la courbe
![\[\psset{xunit=1cm,yunit=3cm,arrowsize=8pt}\begin{pspicture}(-5,-.5)(6,1.2)
\newcommand{\f}[2]{2.718 #1 -1 mul exp #2 mul
1 2.718 -1 #1 mul exp sub #2 1 sub exp mul }
\psline{->}(-.2,0)(6,0)
\psline{->}(0,-.2)(0,1.2)
\psline[linecolor=blue,linewidth=1.5pt](-5,0)(0,0)
\psplot[linecolor=blue,linewidth=1.5pt]{0}{5}{\f{x}{2}}
\psline(-.1,1)(.1,1)\rput[r](-.2,1){1}
\psline(.69,0)(!.69\space\f{.69}{2})(!0\space\f{.69}{2})\rput(.69,-.1){\blue$\ln2$}
%n=5 et ln(5)~1.61
\psline[linecolor=red,linewidth=1.2pt](-5,0.01)(0,0.01)
\psplot[linecolor=red,linewidth=1.5pt]{0}{5}{\f{x}{5}}
\psline(1.61,0)(!1.61\space\f{1.61}{5})(!0\space\f{1.61}{5})\rput(1.61,-.1){\red$\ln5$}
\rput(.7,.6){\blue$n\!=\!2$}
\rput(4.2,.2){\red$n\!=5\!$}
\end{pspicture}\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/22.png)
- La fonction à intégrer est continue sur
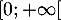 , et seule la convergence en l'infini est donc éventuellement problématique.
, et seule la convergence en l'infini est donc éventuellement problématique.
En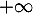 on a
on a 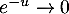 et
l'équivalent
et
l'équivalent 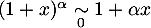 donne alors
donne alors
![\[1-\lp1-e^{-u}\rp^n\underset{0}{\sim}ne^{-u}\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/27.png)
qui est intégrable en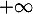 ,
par exemple par critère de Riemann car
,
par exemple par critère de Riemann car 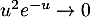 par croissances comparées.
par croissances comparées.
L'intégrale converge donc bien. - En utilisant la formuel de l'énoncé, on a
![\[\begin{array}{lcl}
E\left[ M_n\rp&=&\dsp\int_0^{+\infty}P\left( M_n\geqslant u\rp\,du\\[1em]
&=&\dsp\int_0^{+\infty}\left( 1-P\left( M_n< u\rp\rp\,du\\[1em]
&=&\dsp\int_0^{+\infty}\left( 1-\left(1-e^{-u}\rp^n\rp\,du
\enar\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/30.png)
qui est l'intégrale convergente de la question précédente.
On effectue le changement de variable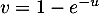 , avec
, avec 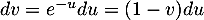 et alors
et alors
![\[\int_0^{+\infty}\left( 1-\left(1-e^{-u}\rp^n\rp\,du
=\int_0^1\dfrac{1-v^n}{1-v}\,dv\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/33.png)
Le terme à intégrer est la somme des termes d'une suite géométrique:
![\[\dfrac{1-v^n}{1-v}=\sum_{k=0}^{n-1}v^k\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/34.png)
et donc, par linéarité de l'intégrale,
![\[\begin{array}{lcl}
E\left[ M_n\right]
&=&\dsp\int_0^{+\infty}\left( 1-\left(1-e^{-u}\rp^n\rp\,du\\[1.2em]
&=&\dsp\sum_{k=0}^{n-1}\int_0^1v^k\,dv\\[1.2em]
&=&\dsp\sum_{k=0}^{n-1}\dfrac1{k+1}\\[1.2em]
&=&\dsp\sum_{k=1}^n\dfrac1k
\enar\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/35.png)
qui est la somme partielle de la série harmonique donc on sait qu'elle diverge vers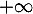 avec, plus précisément
avec, plus précisément
![\[\sum_{k=1}^n\dfrac1k\underset{+\infty}{\sim}\ln(n)\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/37.png)
On trouve donc finalement que
![\[\lim_{n\to+\infty}\dfrac{E\left[ M_n\right]}{\ln(n)}=1\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/38.png)
Remarque: À savoir démontrer (question bonus ?): la formule donnée dans l'énoncé pour le calcul de l'espérance, et l'équivalent pour la série harmonique.
- Formule pour l'espérance
Soit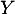 une variable aléatoire sur
une variable aléatoire sur 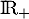 , de densité
, de densité 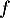 et de fonction de répartition
et de fonction de répartition 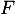 définie par
définie par 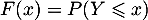 .
.
Comme le suggère la formule souhaitée, on passe par l'événement contraire en posant
![\[G(x)=P(Y>x)=1-F(x)\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/44.png)
On a alors,
![\[\begin{array}{lcl}E[Y]&=&\dsp\int_0^{+\infty}xf(x)\,dx\\
&&=\dsp\int_0^{+\infty}xF'(x)\,dx\\
&&=\dsp-\int_0^{+\infty}xG'(x)\,dx\\
\enar\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/45.png)
puis, en intégrant par parties,
![\[\begin{array}{lcl}E[Y]&=&-\bigl[\,xG(x)\,\bigr]_0^{+\infty}+\dsp\int_0^{+\infty}G(x)\,dx\\[1em]
&=&\dsp\int_0^{+\infty}P(Y>x)\,dx\enar\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/46.png)
bien sûr sous réserve que les intégrales considérées convergent et que
![\[\lim_{x\to+\infty}xG(x)=0\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/47.png)
- Équivalent de la série harmonique
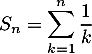
On utilise la comparaison série-intégrale: comme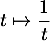 est décroissante, on a
est décroissante, on a
![\[k\leqslant t\leqslant k+1 \iff
\dfrac1{k+1}\leqslant\dfrac1t\leqslant\dfrac1k\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/50.png)
puis en intégrant,
![\[\dfrac1{k+1}\leqslant\int_k^{k+1}\dfrac1t\,dt\leqslant\dfrac1k\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/51.png)
et enfin en sommant,
![\[\sum_{k=1}^n\dfrac1{k+1}
\leqslant\sum_{k=1}^n\int_k^{k+1}\dfrac1t\,dt
\leqslant\sum_{k=1}^n\dfrac1k\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/52.png)
soit,
![\[S_{n+1}\leqslant\int_1^{n+1}\dfrac{dt}{t}=\ln(n+1)\leqslant S_n\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/53.png)
On a donc obtenu que
![\[S_{n+1}\leqslant\ln(n+1)\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/54.png)
soit aussi
![\[S_n\leqslant\ln(n)\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/55.png)
et que
![\[S_n\geqslant\ln(n+1)\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/56.png)
soit, en résumé,
![\[\ln(n+1)\leqslant S_n\leqslant\ln(n)\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/57.png)
et donc,
![\[\dfrac{\ln(n+1)}{\ln(n)}\leqslant\dfrac{S_n}{\ln(n)}\leqslant1\]](/Generateur-Devoirs/Colles/VAC/EmaxE_c/58.png)
et on obtient la limite et l'équivalent grâce au théorème des gendarmes.
- Formule pour l'espérance
Tag:Variables aléatoires continues
Autres sujets au hasard:
