next_inactive up previous
suivant: Modélisation de la propagation 1-D d'une onde

Discrétisation des équations de la physique - Méthode des différences finies

Approximation de la dérivée d'une fonction

Les équations de la physique sont le plus souvent des équations différentielles, ou équations aux dérivées partielles, c'est-à-dire des équations dont l'inconnue est une fonction et qui font intervenir cette fonction recherchée ainsi que ses dérivées (dérivées première, seconde, ...).


Par exemple, l'équation: \fbox{ $(\mathcal{E}) : \left\{\begin{array}{ll} f'(x)=f(x)$, pour tout $x\in[\,0\,;1\,] \vspace{0.2cm}\\ f(0)=1 \end{array}\right. $} ,


où $ f$ est la fonction recherchée, est une équation différentielle (dite du premier ordre, car ne faisant intervenir que la dérivée première $ f'$ de $ f$ ).


La dérivée d'une fonction $ f$ , que l'on suppose bien sûr dérivable, en $ x$ est la limite du taux de variation de la fonction:

$\displaystyle f'(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h} $

où le quotient $ \displaystyle \frac{f(x+h)-f(x)}{h}$ est le taux de variation en $ x$ de la fonction $ f$ .


Ainsi la dérivée en $ x$ , $ f'(x)$ , est un taux de variation infinitésimal.


La méthode dite des différences finies propose simplement de remplacer ces taux de varations infinitésimaux par des taux de variations finis (la qualification de "fini" est faite par opposition à infiniment petits).

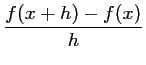
$\displaystyle \frac{f(x+h)-f(x)}{h} $

L'approximation ainsi réalisée étant bien évidemment d'autant meilleure que le pas $ h$ est choisi petit.



Maillage du domaine ou de l'intervalle d'étude

Imaginons que l'on ne connaisse pas la fonction solution de l'équation $ (\mathcal{E})$ , ou que l'on ne sache pas l'exprimer à l'aide de fonctions usuelles.

On peut néanmoins alors tenter calculer des valeurs approchées de $ f(x)$ .


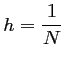On découpe tout d'abord l'intervalle du problème, ici $ [\,0\,;1\,]$ en $ N$ intervalles, chacun de longueur $ \displaystyle h=\frac{1}{N}$ . On numérote chacun des points obtenus: $ x_0$ , $ x_1$ , $ x_2$ , ..., $ x_{N-1}$ , $ x_N$ .


\begin{pspicture}(-2,-1)(15,2) \psline[linewidth=1.5pt]{->}(-1,0)(13,0) \multi... ...$} \psline[linewidth=1pt]{->}(7,0.7)(7.95,0.7)\rput(7.5,1){$h$} \end{pspicture}


La suite des abscisses est une suite arithmétique de raison $ h$ :

$\displaystyle x_1=x_0+h\ \ , \ \ x_2=x_1+h\ \ , \ \ \dots\ \ , \ \ x_{n+1}=x_n+h$

et donc, pour tout entier $\displaystyle n\ ,\ \ \underline {x_n=x_0+nh}.$


Ce découpage de l'intervalle $ [\,0\,;1\,]$ s'appelle une discrétisation, ou un maillage de l'intervalle.



Discrétisation des équations différentielles


Résoudre numériquement l'équation $ (\mathcal{E})$ signifie maintenant déterminer des valeurs approchées de $ f(x_0)$ , $ f(x_1)$ , $ f(x_2)$ , ..., $ f(x_N)$ .


Pour simplifier un peu les notations, on introduit la suite $ (u_n)$ définie par

$\displaystyle u_n=f(x_n)\ , \ $    ou encore, d'après la défintion de la suite $\displaystyle x_n\ , \ u_n=f(x_0+nh) $

Une valeur approchée de la dérivée $ f'(x_n)$ est donnée par le taux de variation de $ f$ en $ x_n$ (en choisissant un pas $ h$ assez petit):

$\displaystyle f'(x_n)\simeq \frac{f(x_n+h)-f(x_n)}{h} =\frac{f(x_{n+1})-f(x_n)}{h} $

ou encore, avec la suite introduite précédemment:

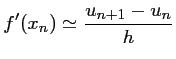
$\displaystyle f'(x_n)\simeq \frac{u_{n+1}-u_n}{h} $

L'équation de départ $ (\mathcal{E})$ nous dit que, pour tout $ x\in[\,0\,;1\,]$ , $ f'(x)=f(x)$ , donc aussi, pour tout entier $ n\leq N$ , $ f'(x_n)=f(x_n)$ , soit

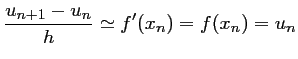
$\displaystyle \frac{u_{n+1}-u_n}{h} \simeq f'(x_n)=f(x_n)=u_n $

On aboutit ainsi à la relation de récurrence:

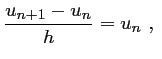$\displaystyle \frac{u_{n+1}-u_n}{h}=u_n\ ,\ $    soit aussi, $\displaystyle \underline {u_{n+1}=(1+h)u_n} $

Finalement, la discrétisation de l'équation différentielle $ (\mathcal{E})$ s'écrit:

$\displaystyle \left\{\begin{array}{ll} u_0=f(0)=1 \vspace{0.2cm}\\ \displaysty... ...=(1+h)u_n \ , \ \mbox{pour tout entier } n\leq N=\frac{1}{h}\end{array}\right. $

Cette dernière relation nous permet de calculer tous les termes de la suite $ u_n$ , donc toutes les valeurs approchées prises par la fonction $ f(x_n)$ .



Application numérique

Pour $ N=10$ par exemple, soit un pas $ h=0,1$ , on obtient:

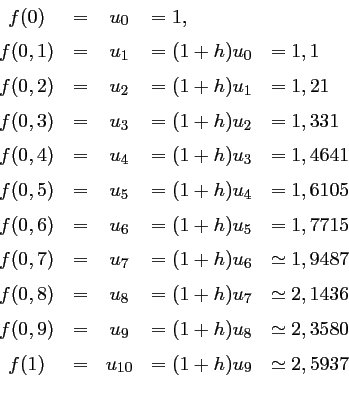
\begin{displaymath}\begin{array}{clcll} f(0) &= &u_0&=1, \vspace{0.2cm}\\ f(0,1... ...&=&u_{10}&=(1+h)u_9&\simeq 2,5937 \vspace{0.2cm}\\ \end{array}\end{displaymath}

Il se trouve que pour l'équation $ (\mathcal{E})$ , la solution est en fait connue, il s'agit de la fonction exponentielle: $ f(x)=\exp(x)$ .

On a donc ainsi une bonne occasion d'observer l'efficacité de la méthode, en comparant les résultats approchés obtenus ci-dessus aux valeurs exactes.

Cette comparaison est effectuée sur le graphique suivant.

\epsfbox{PlotSol}

Représentation graphique de la solution, exacte en rouge, approchée (suite $ (u_n)$ ) en noir.



Pour aller plus loin: formules de Taylor

L'expression utilisée pour approximer la dérivée était:

$\displaystyle f'(x)\simeq \frac{f(x+h)-f(x)}{h} $

dans la mesure où $ h$ (le pas de la discrétisation) est un nombre petit.


Cette expression peut se réécrire sous la forme,

$\displaystyle f(x+h)\simeq f(x)+ hf'(x) $

Cette expression est plus précisément la formule de Taylor, au premier ordre (l'ordre de grandeur de l'approximation est donné par le paramètre $ h=h^1$ à la puissance 1).


De manière plus générale, si on suppose la fonction $ n$ fois dérivable (la fonction $ f$ est dérivable de dérivée $ f'$ , $ f'$ étant dérivable de dérivée $ (f')'=f''$ , qui est elle même dérivable de dérivée $ (f'')'$ , ..., et ainsi de suite $ n$ fois), alors la formule de Taylor à l'ordre $ n$ s'écrit:

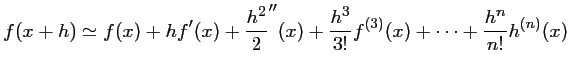
$\displaystyle f(x+h)\simeq f(x)+hf'(x)+\frac{h^2}{2}''(x)+\frac{h^3}{3!}f^{(3)}(x) +\dots + \frac{h^n}{n!}h^{(n)}(x) $

où, $ n!=n\times (n-1)\times (n-2)\times \dots3\times 2\times 1$ désigne factorielle $ n$ , et $ f^{(n)}$ désigne la dérivée n-ième de $ f$ ( $ f^{(1)}=f'$ , $ f^{(2)}=(f')'=f''$ , $ f^{(3)}=(f^{(2)})'$ , ...)


En utilisant cette formule, on peut alors donner une approximation, par exemple de la dérivée seconde de $ f$ , en remplaçant $ h$ par $ -h$ dans la formule à l'ordre 2:

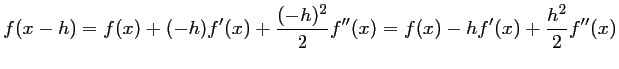
$\displaystyle f(x-h)=f(x)+(-h)f'(x)+\frac{(-h)^2}{2}f''(x) =f(x)-hf'(x)+\frac{h^2}{2}f''(x) $

puis en ajoutant les relations donnant $ f(x+h)$ et $ f(x-h)$ :

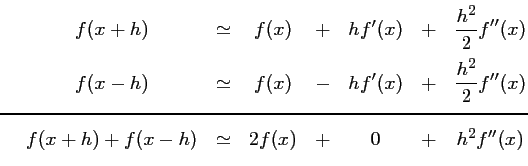
\begin{displaymath} \begin{array}{clclclc} f(x+h)&\simeq &f(x) &+ &hf'(x) &+ &\d... ....6) f(x+h)+f(x-h)&\simeq &2f(x) &+ &0 &+ &h^2f''(x) \end{array}\end{displaymath}

d'où,

$\displaystyle f''(x)\simeq \frac{f(x+h)+f(x-h)-2f(x)}{h^2} $

et, avec les suites introduites précédemment ($ x_n$ et $ u_n=f(x_n)$ ),

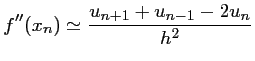
$\displaystyle f''(x_n)\simeq \frac{u_{n+1}+u_{n-1}-2u_n}{h^2} $

On obtient ainsi une approximation de la dérivée seconde de la fonction.


Cette approximation rend accessible le calcul approchée des équations différentielles du second ordre, et en particulier les équations de la mécanique (la relation fondamentale de la mécanique, $ \overrightarrow{F}=m\vec{a}$ , où $ \vec{a}$ est l'accélération, donc la dérivée seconde de la position de l'objet ...)


De très nombreuses autres équations font intervenir les dérivées secondes des fonctions recherchées; c'est le cas entre autre de l'équation des ondes décrivant, comme son nom l'indique, la propagation d'une onde acoustique ou électromagnétique.


suivant: Modélisation de la propagation 1-D d'une onde

Voir aussi: Méthodes numériques pour la résolution de problèmes Lien

LongPage: h2: 5 - h3: 0