|
suivant: Méthodes numériques |
Reconstruction d'un sinal numérisé
Conversion analogique / numétique
|
Un problème fondamental
qui se pose après numérisation d'un signal
est :
est-il possible de retrouver, à partir des seuls échantillons
numériques disponibles, le signal original (analogique) complet ?
D'après l'analyse de Fourier, tout signal peut-être décomposé en une somme (infinie) de signaux élémentaires purement sinusoïdaux. La question peut alors se reformuler ainsi: à quelle(s) condition(s) quelques échantillons permettent-ils de différencier deux signaux sinusoïdaux ? Par exemple, si on ne considère que deux échantillons distants de 0,2s, alors un signal sinusoïdal de fréquence 5 Hz (période T=0,2s) pourra passer par ces échantillons, ainsi qu'un de signal de 10 Hz (période T=0,1s), ou de 20 Hz (T=0,05 s) ... Il existe en fait une infinité sinusoïdes ayant les mêmes échantillons. 

En échantillonnant toutes les
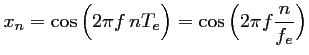
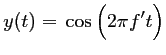
qui donne, après le même échantillonnage que pour
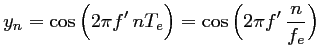
On ne pourra différencier le signal
soit, si
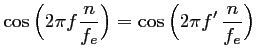
L'égalité des deux cosinus a lieu si les arguments sont égaux modulo
 pour pour
soit aussi,
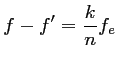
En particulier, dès le premier échantillon (
ce qui est assuré si
ou encore, en utilisant l'inégalité triangulaire (
Finalement, on peut distinguer les deux signaux si on impose la condition sur les fréquences:

En résumé, on distingue clairement deux signaux sinusoïdaux échantillonnés si la fréquence d'échantillonnage utilisée est au moins deux fois supérieure à la plus grande des fréquences des signaux.
Théorème de Shannon:![\fbox{
\begin{minipage}{\textwidth}
Etant donné une suite de valeurs $x_n$\ éc...
...\ dont le spectre est compris
dans l'intervalle $[-f_e;f_e]$.
\end{minipage}}](/MathAppli/Conversion_Analogique_Numerique/FIG/img26.png)
|
suivant: Modélisation et simulation de la propagation d'une onde
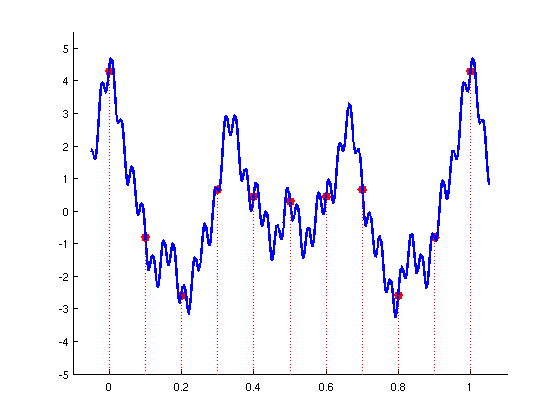
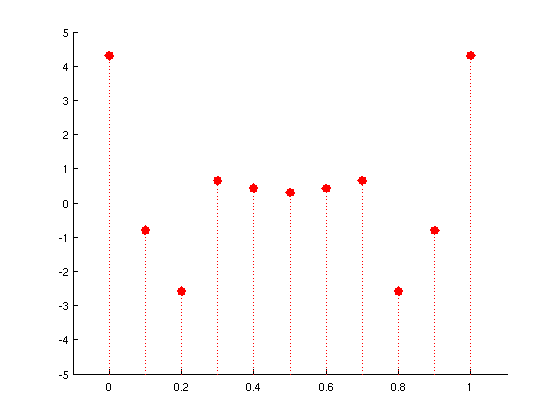
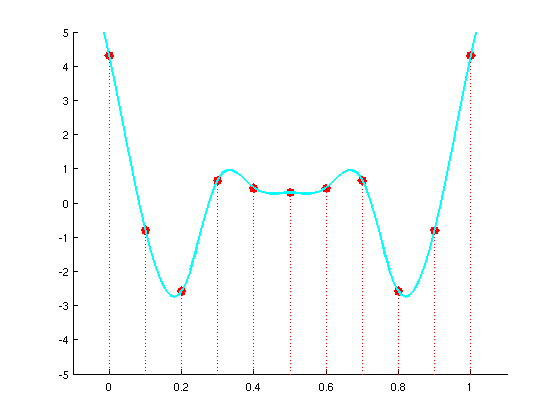
 , on obtient la suite d'échantillons:
, on obtient la suite d'échantillons: