Programmation en Matlab
Fractales Mandelbrot, Julia, Serpinski
Quelques éléments de programmation pour le TP 5: Fractales de Mandelbrot, Julia, Serpinski.Fractale de Mandelbrot
Un exemple de représentation graphique de l'ensemble de Mandelbrot: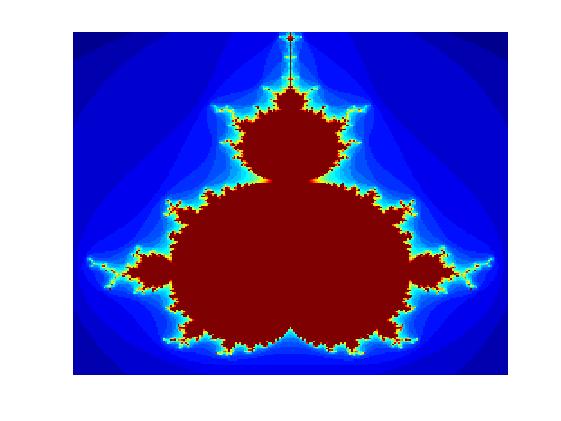
et ci-dessous le code Matlab qui permet de la générer.
clear all;close all % Pour bien commencer...
% Nombre de termes calcules pour chaque suite
Nmax=30;
% Seuil a partir duquel on considere que la suite diverge
Seuil=2;
pasx=0.01;
pasy=0.01;
M=[];
for x=-1.8:pasx:0.6
V=[];
for y=-1.2:pasy:1.2
% Initialisation de la suite
z=0+1i*0;
% Puis on calcule les termes de la suite jusqu'a Nmax
% sauf si on depasse le seuil (on considere alors que la suite
% diverge vers l'infini)
for bcl=0:Nmax
z=z^2+(x+1i*y);
% Test divergence
if abs(z)>Seuil, break;end
end
V=[V, bcl];
%V=[V,abs(z)];
end
M=[M;V];
end
figure(1),clf,whitebg('w');axis off
imagesc(M);
Fractale de Julia
Un exemple de représentation graphique de l'ensemble de Mandelbrot: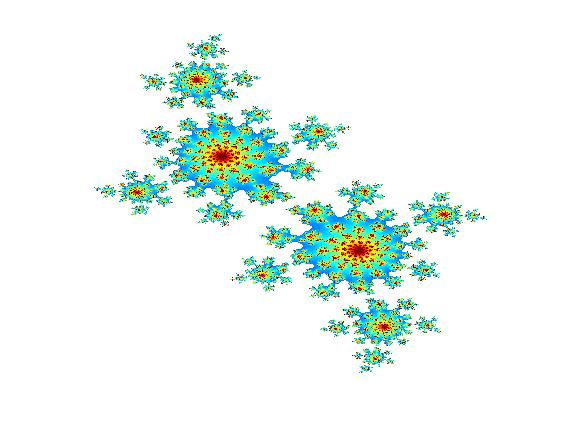
et ci-dessous le code Matlab qui permet de la générer. Bien sûr, il ne faut pas hésiter à jouer avec la valeur du paramètre complexe
c
clear all;close all
% parametre initial: diffentes valeurs possibles bien sur...
%c=-1;
%c=-1+0.2312i
%c=0.112-0.64i
c=-0.414-0.612i
%c=0.284-0.0122i
% Nombre de termes calcules pour chaque suite
Nmax=100;
% Seuil a partir duquel on considere que la suite diverge
Seuil=10;
pasx=0.002;
pasy=0.002;
% Balayages (discetisations) en x et y
XX=-1.4:pasx:1.4;
YY=-1.1:pasy:1.1;
M=[];
for x=XX
V=[];
for y=YY
% Initialisation de la suite
z=x+1i*y;
% Puis on calcule les termes de la suite jusqu'a Nmax
for bcl=0:Nmax
z=z^2+c;
% Test divergence
if abs(z)>Seuil, break;end
end
V=[V, bcl];
%V=[V,abs(z)];
end
M=[M;V];
end
figure(1),clf,
JJ=jet;JJ(1:15,:)=1;
colormap(JJ);
imagesc(M);
axis off,whitebg('w')
Fractale de Sierpinski
Un exemple de représentation graphique de l'ensemble de Mandelbrot:
et ci-dessous le code Matlab qui permet de la générer.
L'algorithme proposé ici est stochastique. Il existe aussi des constructions plus géométriques par exemple.
clear all;close all
figure(1);clf;hold on;axis off
Nmax=10000; % Nombre d iterations
X=[];Y=[];
A=[0;0];B=[1;0];C=[0;1];
% On tire un point au hasard
x=rand(1);y=rand(1);
if (x+y>1),x=x/2;y=y/2;end
for bcl=1:Nmax
% On choisit le point A, B ou C au hasard
tmp=rand(1);
if (tmp<1/3) % alors point A
x=x/2;y=y/2;
elseif (tmp>2/3) % alors point C
x=x/2;y=(1+y)/2;
else % sinon point B
x=(1+x)/2;y=y/2;
end
X=[X x];
Y=[Y y];
end
plot(X,Y,'.');
On peut aussi animer cette construction, en plaçant au fur et à mesure chaque point, et en imposant une courte pause entre deux points.
clear all;close all
figure(1);clf;hold on;axis([0 1 0 1]);axis off
Nmax=10000; % Nombre d iterations
X=[];Y=[];
A=[0;0];B=[1;0];C=[0;1];
% On tire un point au hasard
x=rand(1);y=rand(1);
if (x+y>1),x=x/2;y=y/2;end
for bcl=1:Nmax
% On choisit le point A, B ou C au hasard
tmp=rand(1);
if (tmp<1/3) % point A
x=x/2;y=y/2;
elseif (tmp>2/3) % point C
x=x/2;y=(1+y)/2;
else % point B
x=(1+x)/2;y=y/2;
end
%X=[X x];
%Y=[Y y];
plot(x,y,'.');pause(.01)
end
end
getframe & movie2avi