Devoir corrigé de maths en Terminale générale, spécialité mathématiques
Annale Bac, spé maths - 12 mai 2022
Baccalauréat 12 mai 2022. Sujet posé en spécialité mathématiques, filière générale. Correction détaillée du sujet.Exercice 1: Arbre et loi binomiale
Le coyote est un animal sauvage proche du loup, qui vit en Amérique du Nord.
Dans l'état d'Oklahoma, aux États-Unis, 70 % des coyotes sont touchés par une maladie appelée ehrlichiose.
Il existe un test aidant à la détection de cette maladie. Lorsque ce test est appliqué à un coyote, son résultat est soit positif, soit négatif, et on sait que :
Partie A
Des vétérinaires capturent un coyote d'Oklahoma au hasard et lui font subir un test pour l'ehrlichiose.
On considère les évènements suivants :
On note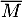 et
et 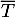 respectivement les évènements contraires de M et T.
respectivement les évènements contraires de M et T.
Partie B
On rappelle que la probabilité qu'un coyote capturé au hasard présente un test positif est de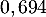 .
.
Dans l'état d'Oklahoma, aux États-Unis, 70 % des coyotes sont touchés par une maladie appelée ehrlichiose.
Il existe un test aidant à la détection de cette maladie. Lorsque ce test est appliqué à un coyote, son résultat est soit positif, soit négatif, et on sait que :
- Si le coyote est malade, le test est positif dans 97 % des cas.
- Si le coyote n'est pas malade, le test est négatif dans 95 % des cas.
Partie A
Des vétérinaires capturent un coyote d'Oklahoma au hasard et lui font subir un test pour l'ehrlichiose.
On considère les évènements suivants :
- M: « le coyote est malade »;
- T: « le test du coyote est positif ».
On note
- Recopier et compléter l'arbre pondéré ci-dessous qui modélise la situation.
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$M$}
\rput(.8,.9){\dots}
\rput(.8,-1){\dots}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{M}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$T$}
\rput(2.8,1.7){\dots}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{T}$}
\rput(2.8,.2){\dots}
\rput(2.8,-.4){\dots}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{T}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$T$}
\rput(2.8,-1.8){\dots}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022/7.png)
- Déterminer la probabilité que le coyote soit malade et que son test soit positif.
- Démontrer que la probabilité de T est égale à
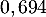 .
.
- On appelle « valeur prédictive positive du test » la probabilité que le coyote soit effectivement malade sachant que son test est positif.
Calculer la valeur prédictive positive du test. On arrondira le résultat au millième. -
- Par analogie avec la question précédente, proposer une définition de la « valeur prédictive négative du test » et calculer cette valeur en arrondissant au millième.
- Comparer les valeurs prédictives positive et négative du test, et interpréter.
Partie B
On rappelle que la probabilité qu'un coyote capturé au hasard présente un test positif est de
- Lorsqu'on capture au hasard cinq coyotes, on assimile ce choix à un tirage avec remise.
On note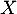 la variable aléatoire qui à un échantillon de cinq coyotes capturés au hasard associe le nombre de coyotes dans cet échantillon ayant un test positif.
la variable aléatoire qui à un échantillon de cinq coyotes capturés au hasard associe le nombre de coyotes dans cet échantillon ayant un test positif.
- Quelle est la loi de probabilité suivie par
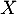 ? Justifier et préciser ses paramètres.
? Justifier et préciser ses paramètres.
- Calculer la probabilité que dans un échantillon de cinq coyotes capturés au hasard, un seul ait un test positif. On arrondira le résultat au centième.
- Un vétérinaire affirme qu'il y a plus d'une chance sur deux qu'au moins quatre coyotes sur cinq aient un test positif : cette affirmation est-elle vraie ? Justifier la réponse.
- Quelle est la loi de probabilité suivie par
- Pour tester des médicaments, les vétérinaires ont besoin de disposer d'un coyote présentant un test positif. Combien doivent-ils capturer de coyotes pour que la probabilité qu'au moins l'un d'entre eux présente un test positif soit supérieure à
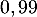 ?
?
Correction exercice 1
Partie A
Partie B
Cacher la correction
Partie A
-
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$M$}
\rput(.8,.9){70\%}
\rput(.8,-1){30\%}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{M}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$T$}
\rput(2.8,1.7){97\%}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{T}$}
\rput(2.8,.4){3\%}
\rput(2.8,-.4){5\%}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{T}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$T$}
\rput(2.8,-1.7){95\%}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/1.png)
- D'après l'arbre, la probabilité que le coyote soit malade
et que son test soit positif est
![\[P(\overline{M}\cap T)=30\%\tm5\%=1,5\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/2.png)
- D'après l'arbre, ou la formule des probabilités totales,
![\[P(T)=70\%\tm97\%+30\%\tm5\%=69,4\%=0,694\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/3.png)
- La valeur prédictive positive du test est la probabilité conditionnelle
![\[P_T(M)=\dfrac{P(M\cap T)}{P(T)}=\dfrac{70\%\tm97\%}{69,4\%}\simeq0,978=97,8\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/4.png)
-
- Par analogie avec la question précédente, la « valeur prédictive négative du test » est la probabilité que le coyote ne soit effectivement pas malade sachant que son test est négatif, et vaut
![\[P_{\overline{T}}(\overline{M})=\dfrac{P(\overline{T}\cap\overline{M})}{P(\overline{T})}
=\dfrac{30\%\tm95\%}{1-0,694}\simeq0,931=93,1\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/5.png)
- La valeur prédictive positive est plus grande que celle négative: le test est donc plus fiable pour diagonostiquer un animal malade qu'un animal sain.
- Par analogie avec la question précédente, la « valeur prédictive négative du test » est la probabilité que le coyote ne soit effectivement pas malade sachant que son test est négatif, et vaut
Partie B
-
- On répète
 fois l'expérience aléatoire "capturer un coyote",
dont le succès est "le coyote a un test positif" de probabilité
fois l'expérience aléatoire "capturer un coyote",
dont le succès est "le coyote a un test positif" de probabilité
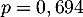 .
Ces répétitions sont identiques et indépendantes (car on l'assimile à un tirage avec remise).
.
Ces répétitions sont identiques et indépendantes (car on l'assimile à un tirage avec remise).
Enfin, la variable aléatoire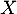 est égale au nombre de succès sur ces 5 répétitions, c'est-à-dire au nombre de coyotes dont le test est positif.
est égale au nombre de succès sur ces 5 répétitions, c'est-à-dire au nombre de coyotes dont le test est positif.
On en déduit que cette variable aléatoire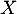 suit la loi binomiale de paramètres
suit la loi binomiale de paramètres
 et
et 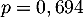 .
.
- La probabilité que dans un échantillon de cinq coyotes capturés au hasard, un seul ait un test positif est, à l'aide de la calculatrice,
![\[P(X=1)\simeq 0,03\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/12.png)
- La probabilité qu'au moins quatre coyotes sur cinq aient un test positif est
![\[P(X\geqslant4)\simeq0,52\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/13.png)
ce qui montre que l'affirmation du vétérinaire est vraie.
- On répète
- On capture donc
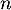 coyotes, et on note
coyotes, et on note 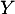 la variable aléatoire égale au
nombre de coyotes ayant un test positif dans cet échantillon.
Comme précédemment,
la variable aléatoire égale au
nombre de coyotes ayant un test positif dans cet échantillon.
Comme précédemment, 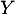 suit la loi binomiale de paramètres
suit la loi binomiale de paramètres 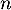 et
et 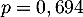 .
.
On cherche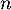 tel que
tel que 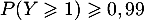
On a
![\[P(Y\geqslant1)=1-P(Y=0)=1-(1-0,694)^n=1-0,306^n\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/21.png)
et donc
![\[\begin{array}{ll}&P(Y\geqslant1)\geqslant0,99\\
\iff& 1-0,306^n\geqslant0,99\\
\iff& 0,306^n\leqslant0,01\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/22.png)
soit, en prenant le logarithme qui est strictement croissant (donc l'ordre est conservé), puis en divisant par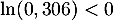 (donc l'ordre est changé):
(donc l'ordre est changé):
![\[\begin{array}{ll}&P(Y\geqslant1)\geqslant0,99\\
\iff&\ln\lp0,306^n\rp=n\ln(0,306)\leqslant\ln(0,01)\\
\iff&n\geqslant\dfrac{\ln(0,01)}{\ln(0,306)}\simeq3,88\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/24.png)
Il faut donc capturer au moins 4 coyote.
Cacher la correction
Exercice 2: QCM: fonctions, convexité, suites
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée.
Pour les questions 1 à 3 ci-dessous, on considère une fonction définie et deux fois dérivable sur
définie et deux fois dérivable sur 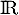 . La courbe de sa fonction dérivée
. La courbe de sa fonction dérivée  est donnée ci-dessous.
est donnée ci-dessous.
On admet que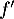 admet un maximum en
admet un maximum en 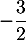 et que sa courbe coupe l'axe des abscisses au point de coordonnées
et que sa courbe coupe l'axe des abscisses au point de coordonnées 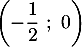 .
.
Question 1 :
a. La fonction admet un maximum en
admet un maximum en 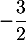
b. La fonction admet un maximum en
admet un maximum en 
c. La fonction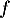 admet un minimum en
admet un minimum en 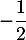
d. Au point d'abscisse , la courbe de la fonction
, la courbe de la fonction 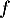 admet une tangente horizontale.
admet une tangente horizontale.
![\[\psset{unit=1.2cm}
\begin{pspicture*}(-5.2,-2.6)(1,1)
\psgrid[gridlabels=0pt,subgriddiv=4,gridwidth=0.25pt,subgridwidth=0.15pt]
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle]{->}(0,0)(-5.2,-2.6)(1,1)
%\pscurve[linecolor=blue,linewidth=1.25pt](-5.2,0.05)(-4,0.13)(-3,0.28)(-2,0.4)(-1,0.35)(0,-1)(0.38,-2.6)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=red]{-5}{3}{2 x mul 1 add 2.71828 x exp mul neg}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/17.png)
Question 2 :
a. La fonction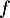 est convexe sur
est convexe sur ![$\left]- \infty~;~- \dfrac32\right[$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/19.png)
b. La fonction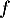 est convexe sur
est convexe sur ![$\left]- \infty;~- \dfrac12\right[$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/21.png)
c. La courbe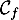 représentant la fonction
représentant la fonction  n'admet pas de point d'inflexion
n'admet pas de point d'inflexion
d. la fonction est concave sur
est concave sur ![$\left] - \infty~;~- \dfrac12\right[$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/25.png)
Question 3:
La dérivée seconde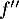 de la fonction
de la fonction 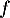 vérifie :
vérifie :
a.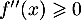 pour
pour ![$x \in \left]-\infty~;~- \dfrac12\right[$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/29.png)
b. pour
pour ![$x \in [- 2~;~- 1]$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/31.png)
c.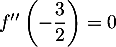
d.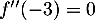
Question 4 :
On considère trois suites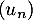 ,
, 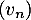 et
et 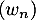 . On sait que, pour tout entier naturel
. On sait que, pour tout entier naturel 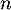 , on a :
, on a : 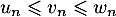 et de plus:
et de plus:  et
et 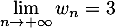 .
.
On peut alors affirmer que :
a. la suite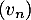 converge
converge
b. Si la suite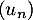 est croissante alors la suite
est croissante alors la suite 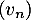 est minorée par
est minorée par 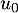
c.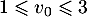
d. la suite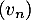 diverge.
diverge.
Question 5:
On considère une suite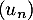 telle que, pour tout entier naturel
telle que, pour tout entier naturel 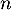 non nul:
non nul: 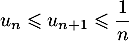 .
.
On peut alors affirmer que :
a. la suite diverge
diverge
b. la suite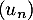 converge
c.
converge
c. d.
d. 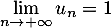 .
.
Question 6:
On considère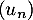 une suite réelle telle que pour tout entier naturel
une suite réelle telle que pour tout entier naturel 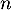 , on a :
, on a : 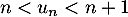 .
.
On peut affirmer que:
a. Il existe un entier naturel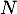 tel que
tel que 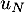 est un entier
est un entier
b. la suite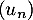 est croissante
est croissante
c. la suite est convergente
est convergente
d. La suite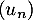 n'a pas de limite.
n'a pas de limite.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée.
Pour les questions 1 à 3 ci-dessous, on considère une fonction
On admet que
Question 1 :
a. La fonction
b. La fonction
c. La fonction
d. Au point d'abscisse
On rappelle que la courbe ci-dessous représente la fonction dérivée 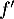 de
de 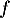 .
.
![\[\psset{unit=1.2cm}
\begin{pspicture*}(-5.2,-2.6)(1,1)
\psgrid[gridlabels=0pt,subgriddiv=4,gridwidth=0.25pt,subgridwidth=0.15pt]
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle]{->}(0,0)(-5.2,-2.6)(1,1)
%\pscurve[linecolor=blue,linewidth=1.25pt](-5.2,0.05)(-4,0.13)(-3,0.28)(-2,0.4)(-1,0.35)(0,-1)(0.38,-2.6)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=red]{-5}{3}{2 x mul 1 add 2.71828 x exp mul neg}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/17.png)
Question 2 :
a. La fonction
b. La fonction
c. La courbe
d. la fonction
Question 3:
La dérivée seconde
a.
b.
c.
d.
Question 4 :
On considère trois suites
On peut alors affirmer que :
a. la suite
b. Si la suite
c.
d. la suite
Question 5:
On considère une suite
On peut alors affirmer que :
a. la suite
b. la suite
Question 6:
On considère
On peut affirmer que:
a. Il existe un entier naturel
b. la suite
c. la suite
d. La suite
Correction exercice 2
Question 1 : b.
Pour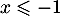 , on a
, on a 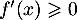 donc
donc 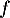 est croissante,
et inversement ensuite pour
est croissante,
et inversement ensuite pour 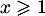 .
.
Ainsi, a un maximum local en
a un maximum local en 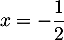 .
.
Question 2 : a.
La dérivée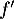 est croissante sur
est croissante sur ![$\left]- \infty~;~- \dfrac32\right[$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/8.png) ,
donc
,
donc 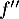 est positive sur cet intervalle, et
est positive sur cet intervalle, et 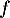 y est convexe.
y est convexe.
Question 3: c.
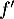 admet un maximum en
admet un maximum en  , donc sa dérivée
, donc sa dérivée  s'y annule.
s'y annule.
Question 4 : b.
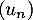 croissante signifie que
croissante signifie que
![\[u_0\leqslant u_1\leqslant u_2\leqslant \dots\leqslant u_n\leqslant\dots\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/15.png)
et on a donc, pour tout entier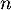 ,
,
![\[u_0\leqslant u_n\leqslant v_n\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/17.png)
ce qui montre que est minorée par
est minorée par 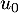 .
.
Question 5: b.
Les inégalités données montrent que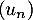 est croissante et aussi aue
est croissante et aussi aue  est majorée, par 1 par exemple, car
est majorée, par 1 par exemple, car
![\[u_n\leqslant u_{n+1}\leqslant\dfrac1n\leqslant1\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/22.png)
Ainsi est convergente (théorème de convergence monotone)
est convergente (théorème de convergence monotone)
Question 6: b.
On a
![\[n < u_n < n + 1\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/24.png)
donc, au rang suivant
![\[n+1 < u_{n+1} < n + 2\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/25.png)
et donc, en particulier
![\[u_n<n+1<u_{n+1}\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/26.png)
qui montre que la suite est croissante.
Cacher la correction
Question 1 : b.
Pour
Ainsi,
Question 2 : a.
La dérivée
Question 3: c.
Question 4 : b.
et on a donc, pour tout entier
ce qui montre que
Question 5: b.
Les inégalités données montrent que
Ainsi
Question 6: b.
On a
donc, au rang suivant
et donc, en particulier
qui montre que la suite est croissante.
Cacher la correction
Exercice 3: Un peu de tout dans l'espace
On considère un cube ABCDEFGH
et on appelle K le milieu du segment [BC].
On se place dans le repère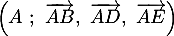 et on considère le tétraèdre EFGK.
et on considère le tétraèdre EFGK.
On rappelle que le volume d'un tétraèdre est donné par:
![\[V=\dfrac13\tm\mathcal{B}\tm h\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022/2.png)
où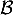 désigne l'aire d'une base et
désigne l'aire d'une base et 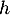 la hauteur relative à cette base.
la hauteur relative à cette base.
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
$$](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022/5.png)
On se place dans le repère
On rappelle que le volume d'un tétraèdre est donné par:
où
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
$$](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022/5.png)
- Préciser les coordonnées des points E, F, G et K.
- Montrer que le vecteur
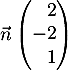 est orthogonal au plan (EGK).
est orthogonal au plan (EGK).
- Démontrer que le plan (EGK) admet pour équation cartésienne :
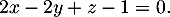
- Déterminer une représentation paramétrique de la droite
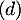 orthogonale au plan (ECK)
passant par F.
orthogonale au plan (ECK)
passant par F.
- Montrer que le projeté orthogonal L de F sur le plan (EGK) a pour coordonnées
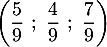 .
.
- Justifier que la longueur LF est égale à
 .
.
- Calculer l'aire du triangle EFG. En déduire que le volume du tétraèdre EFGK est égal à
 .
.
- Déduire des questions précédentes l'aire du triangle EGK.
- On considère les points P milieu du segment [EG], M milieu du segment [EK] et N milieu du segment[GK]. Déterminer le volume du tétraèdre FPMN.
Correction exercice 3
Cacher la correction
- E( 0 ; 0; 1) ; F( 1 ; 0; 1) ;
G( 1 ; 1 ; 1) ; K( 1 ; 0,5 ; 0)
- On a
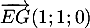 et
et 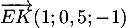 qui sont non colinéaires, et tels que
qui sont non colinéaires, et tels que
![\[\vec{n}\cdot\overrightarrow{EG}=2\tm1+(-2)\tm1+1\tm0=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/3.png)
et
![\[\vec{n}\cdot\overrightarrow{EK}=2\tm1+(-2)\tm0,5+1\tm(-1)=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/4.png)
et donc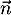 est orthogonal à deux vecteurs colinéaires du plan
(EGK) et donc
est orthogonal à deux vecteurs colinéaires du plan
(EGK) et donc 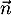 est orthogonal au plan (EGK).
est orthogonal au plan (EGK).
- On déduit de la question précédente qu'une équation cartésienne du plan (EGK)
s'écrit sous la forme
![\[2x-2y+z+d=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/7.png)
De plus,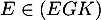 ,
d'où
,
d'où 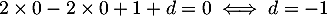 ,
et donc le plan (EGK)
admet bien pour équation cartésienne :
,
et donc le plan (EGK)
admet bien pour équation cartésienne : 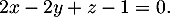
- La droite
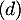 orthogonale au plan (ECK) admet donc
orthogonale au plan (ECK) admet donc 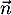 pour vecteur directeur et comme elle passe de plus par F, on peut écrire la représentation paramétrique
pour vecteur directeur et comme elle passe de plus par F, on peut écrire la représentation paramétrique
![\[\la\begin{array}{lclcl}x&=&1&+&2t\\y&=&&-&2t\\z&=&1&+&t\enar\right. \ , \ t\in\R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/13.png)
- Comme
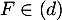 et
et 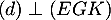 , le projeté orthogonal L de F
sur le plan (EGK) est l'intersection de la droite et du plan.
, le projeté orthogonal L de F
sur le plan (EGK) est l'intersection de la droite et du plan.
En particulier les coordonnées de L vérifient la représentation paramétrique précédente, pour un certain paramètre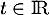 , et aussi l'équation du plan (EGK),
soit
, et aussi l'équation du plan (EGK),
soit
![\[\begin{array}{ll}&2x-2y+z-1=0\\
\iff&2(1+2t)-2(-2t)+(1+t)-1=0\\
\iff&t=-\dfrac29
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/17.png)
d'où les coordonnées de L:
![\[\la\begin{array}{lclclcl}x&=&1&+&2\lp-\dfrac29\rp&=&\dfrac59\\
y&=&&-&2\lp-\dfrac29\rp&=&\dfrac49\\
z&=&1&+&\lp-\dfrac29\rp&=&\dfrac79\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/18.png)
qui sont bien les coordonnées recherchées. -
![\[\begin{array}{ll}LF&=\sqrt{\lp\dfrac59-1\rp^2+\lp\dfrac49-0\rp^2+\lp\dfrac79-1\rp^2}\\[1.4em]
&=\sqrt{\dfrac{4^2+4^2+2^2}{9^2}}
=\sqrt{\dfrac{36}{9^2}}=\sqrt{\dfrac{4}{9}}=\dfrac23
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/19.png)
- Le triangle EFG est isocèle rectangle et a pour aire
![\[\mathcal{A}_{EFG}=\dfrac12EF\times EG=\dfrac12\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/20.png)
Dans le tétraèdre EFGK, la hauteur associée à la base EFG est KK',
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
\psline[linecolor=red,linewidth=1.8pt](4.35,1.05)(4.35,4.55)
\rput(4.2,4.7){K'}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/21.png)
On a KK'=1 et donc le volume
![\[\begin{array}{ll}\mathcal{V}_{EFGK}&=\dfrac13\tm\mathcal{A}_{AEFG}\tm KK'\\[1em]
&=\dfrac13\tm\dfrac12\tm1=\dfrac16\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/22.png)
- On eput aussi calculer ce volume en prenant la base EGK,
la hauteur associée étant alors LF, et on a donc
![\[\begin{array}{ll}&\mathcal{V}_{EFGK}=\dfrac13\tm\mathcal{A}_{EGK}\tm LF\\
\iff& \dfrac16=\dfrac13\tm\mathcal{A}_{EGK}\tm\dfrac23\\
\iff&\mathcal{A}_{EGK}=\dfrac34
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/23.png)
-
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
%
\pspolygon[linecolor=blue](2.6,4.55)(2.275,2.375)(4.675,3.225)%PMN
\psline[linecolor=blue](2.6,4.55)(3.7,3.7)
\psline[linecolor=blue](2.275,2.375)(3.7,3.7)
\psline[linecolor=blue](4.675,3.225)(3.7,3.7)
\rput(2.4,4.7){\blue P}
\rput(2,2.2){\blue M}
\rput(4.84,3.){\blue N}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/24.png)
Comme les deux triangles EGK et PMN sont dans le même plan, les hauteurs qui leurs sont associées dans les deux trétraèdres sont les mêmes, soit LF.
D'arpès le théorème de Thalès, on a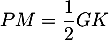 ,
,
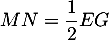 et
et 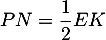 : les longueurs de tous les côtés sont divisées par 2, et l'aire est donc divisée par 4.
: les longueurs de tous les côtés sont divisées par 2, et l'aire est donc divisée par 4.
Finalement, on obtient l'aire du tétraèdre:
![\[\begin{array}{ll}
\mathcal{V}_{FPMN}&=\dfrac13\tm\mathcal{A}_{PMN}\tm LF\\
&=\dfrac13\tm\lp\dfrac14\tm\dfrac34\rp\tm\dfrac23\\
&=\dfrac1{24}
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/28.png)
Cacher la correction
Exercice 4: Trajectoire d'une balle de golf
Partie A : études de deux fonctions
On considère les deux fonctions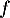 et
et 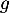 définies sur l'intervalle
définies sur l'intervalle 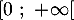 par:
par:
![\[f(x) = 0,06\left(-x^2 +13,7x\right)\quad \text{et}\quad g(x) = (-0,15x + 2,2)e^{0,2x} - 2,2.\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/4.png)
On admet que les fonctions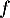 et
et 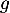 sont dérivables et on note
sont dérivables et on note 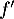 et
et 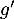 leurs fonctions dérivées respectives.
leurs fonctions dérivées respectives.
Partie B : trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club» de golf.
On souhaite exploiter les fonctions et
et 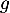 étudiées en Partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
étudiées en Partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
On admettra ici que est la valeur qui annule la fonction
est la valeur qui annule la fonction  et une approximation de la valeur qui annule la fonction
et une approximation de la valeur qui annule la fonction  .
.
On donne ci-dessous les représentations graphiques de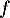 et
et 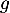 sur l'intervalle [0 ; 13,7].
sur l'intervalle [0 ; 13,7].
![$$(-1,-1)(14,3.5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.2pt]
\psaxes[linewidth=1.25pt,Dx=20,Dy=20]{->}(0,0)(-1,-1)(14,3.5)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}\uput[ur](12,2.2){\blue $\mathcal{C}_g$}
\uput[dl](0,0){0}\uput[d](1,0){1}\uput[l](0,1){1}\uput[d](13.7,0){13,7}
$$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/34.png)
Pour représentant la distance horizontale parcourue par la balle en dizaine de yards après la frappe, (avec
représentant la distance horizontale parcourue par la balle en dizaine de yards après la frappe, (avec  ),
),  (ou
(ou 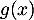 selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaine de yards (1 yard correspond à environ
selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaine de yards (1 yard correspond à environ 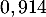 mètre).
mètre).
On appelle « angle de décollage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (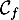 ou
ou 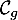 selon le modèle) en son point d'abscisse
selon le modèle) en son point d'abscisse 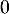 . Une mesure de l'angle de décollage de la balle est
un nombre réel
. Une mesure de l'angle de décollage de la balle est
un nombre réel 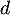 tel que
tel que 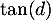 est égal au coefficient directeur de cette tangente.
est égal au coefficient directeur de cette tangente.
De même, on appelle « angle d'atterrissage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (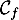 ou
ou 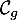 selon le modèle) en son point d'abscisse
selon le modèle) en son point d'abscisse  . Une mesure de l'angle d'atterrissage de la balle est un nombre réel
. Une mesure de l'angle d'atterrissage de la balle est un nombre réel 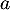 tel que
tel que 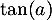 est égal à l'opposé du coefficient directeur de cette tangente.
est égal à l'opposé du coefficient directeur de cette tangente.
Tous les angles sont mesurés en degré.
(-0.3,-0.3)(14,3)
\psplot[plotpoints=1000]{0}{2}{0.822 x mul}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psline(13.7,0)(11,2)
\psarc(0,0){0.7}{0}{40}\rput(1.2,0.5){\footnotesize $d$}
\psarc(13.7,0){0.7}{140}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}&\psset{unit=0.5cm}
\begin{pspicture}(-0.3,-0.75)(14,3.5)
%\psgrid
\psaxes[linewidth=1.25pt,Dx=20,Dy=10](0,0)(-0.3,-0.5)(14,3)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}
\psline(0,0)(10.4,2.8)
\psline(13.7,0)(12,2.9)
\psarc(0,0){1}{0}{20}\rput(2,0.25){\footnotesize $d$}
\psarc(13.7,0){1}{120}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/50.png)
Partie C : interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants:
![\[\begin{tabular}{|*4{p{4.2cm}|}}\hline
Angle de d\'ecollage en degr\'e
&Hauteur maximale en yard
&Angle d'atterrissage en degr\'e
&Distance horizontale en yard au point de chute\\ \hline
24&32&52&137\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/61.png)
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée. Partie A : études de deux fonctions
On considère les deux fonctions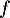 et
et 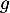 définies sur l'intervalle
définies sur l'intervalle  par:
par:
![\[f(x) = 0,06\left(-x^2 +13,7x\right)\quad \text{et}\quad g(x) = (-0,15x + 2,2)e^{0,2x} - 2,2.\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/65.png)
On admet que les fonctions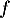 et
et 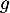 sont dérivables et on note
sont dérivables et on note  et
et 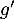 leurs fonctions dérivées respectives.
leurs fonctions dérivées respectives.
Partie B : trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club» de golf.
On souhaite exploiter les fonctions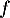 et
et  étudiées en Partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
étudiées en Partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
On admettra ici que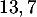 est la valeur qui annule la fonction
est la valeur qui annule la fonction 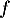 et une approximation de la valeur qui annule la fonction
et une approximation de la valeur qui annule la fonction 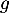 .
.
On donne ci-dessous les représentations graphiques de et
et 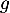 sur l'intervalle [0 ; 13,7].
sur l'intervalle [0 ; 13,7].
![$$(-1,-1)(14,3.5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.2pt]
\psaxes[linewidth=1.25pt,Dx=20,Dy=20]{->}(0,0)(-1,-1)(14,3.5)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}\uput[ur](12,2.2){\blue $\mathcal{C}_g$}
\uput[dl](0,0){0}\uput[d](1,0){1}\uput[l](0,1){1}\uput[d](13.7,0){13,7}
$$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/95.png)
Pour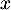 représentant la distance horizontale parcourue par la balle en dizaine de yards après la frappe, (avec
représentant la distance horizontale parcourue par la balle en dizaine de yards après la frappe, (avec  ),
),  (ou
(ou 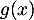 selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaine de yards (1 yard correspond à environ
selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaine de yards (1 yard correspond à environ 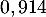 mètre).
mètre).
On appelle « angle de décollage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (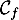 ou
ou  selon le modèle) en son point d'abscisse
selon le modèle) en son point d'abscisse 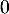 . Une mesure de l'angle de décollage de la balle est
un nombre réel
. Une mesure de l'angle de décollage de la balle est
un nombre réel 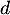 tel que
tel que 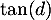 est égal au coefficient directeur de cette tangente.
est égal au coefficient directeur de cette tangente.
De même, on appelle « angle d'atterrissage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (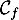 ou
ou 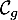 selon le modèle) en son point d'abscisse
selon le modèle) en son point d'abscisse 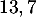 . Une mesure de l'angle d'atterrissage de la balle est un nombre réel
. Une mesure de l'angle d'atterrissage de la balle est un nombre réel  tel que
tel que  est égal à l'opposé du coefficient directeur de cette tangente.
est égal à l'opposé du coefficient directeur de cette tangente.
Tous les angles sont mesurés en degré.
(-0.3,-0.3)(14,3)
\psplot[plotpoints=1000]{0}{2}{0.822 x mul}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psline(13.7,0)(11,2)
\psarc(0,0){0.7}{0}{40}\rput(1.2,0.5){\footnotesize $d$}
\psarc(13.7,0){0.7}{140}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}&\psset{unit=0.5cm}
\begin{pspicture}(-0.3,-0.75)(14,3.5)
%\psgrid
\psaxes[linewidth=1.25pt,Dx=20,Dy=10](0,0)(-0.3,-0.5)(14,3)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}
\psline(0,0)(10.4,2.8)
\psline(13.7,0)(12,2.9)
\psarc(0,0){1}{0}{20}\rput(2,0.25){\footnotesize $d$}
\psarc(13.7,0){1}{120}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/111.png)
Partie C : interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants:
![\[\begin{tabular}{|*4{p{4.2cm}|}}\hline
Angle de d\'ecollage en degr\'e
&Hauteur maximale en yard
&Angle d'atterrissage en degr\'e
&Distance horizontale en yard au point de chute\\ \hline
24&32&52&137\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/122.png)
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée.
On considère les deux fonctions
On admet que les fonctions
- On donne le tableau de variations complet de la fonction
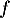 sur l'intervalle
sur l'intervalle 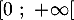 .
.
{$x$} \uput[u](1.6,1.4){$0$} \uput[u](4,1.4){$6,85$} \uput[u](6,1.4){$+ \infty$}
\rput(0.75,0.75){$f(x)$}\uput[u](1.65,0){$0$}\uput[d](4,1.5){$f(6,85)$}\uput[u](6,0){$- \infty$}
\psline{->}(1.9,0.4)(3.2,1.1)\psline{->}(4.8,1.1)(5.7,0.4)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/11.png)
- Justifier la limite de
 en
en  .
.
- Justifier les variations de la fonction
 .
.
- Résoudre l'équation
 .
.
- Justifier la limite de
-
- Déterminer la limite de
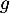 en
en  .
.
- Démontrer que, pour tout réel
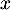 appartenant à
appartenant à 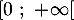 on a :
on a :  .
.
- Étudier les variations de la fonction
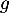 et dresser son tableau de variations sur
et dresser son tableau de variations sur 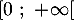 .
.
Préciser une valeur approchée à près du maximum de
près du maximum de 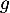 .
.
- Montrer que l'équation
 admet une unique solution non nulle et déterminer, à
admet une unique solution non nulle et déterminer, à  près, une valeur approchée de cette solution.
près, une valeur approchée de cette solution.
- Déterminer la limite de
Partie B : trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club» de golf.
On souhaite exploiter les fonctions
On admettra ici que
On donne ci-dessous les représentations graphiques de
![$$(-1,-1)(14,3.5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.2pt]
\psaxes[linewidth=1.25pt,Dx=20,Dy=20]{->}(0,0)(-1,-1)(14,3.5)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}\uput[ur](12,2.2){\blue $\mathcal{C}_g$}
\uput[dl](0,0){0}\uput[d](1,0){1}\uput[l](0,1){1}\uput[d](13.7,0){13,7}
$$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/34.png)
Pour
On appelle « angle de décollage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (
De même, on appelle « angle d'atterrissage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (
Tous les angles sont mesurés en degré.
(-0.3,-0.3)(14,3)
\psplot[plotpoints=1000]{0}{2}{0.822 x mul}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psline(13.7,0)(11,2)
\psarc(0,0){0.7}{0}{40}\rput(1.2,0.5){\footnotesize $d$}
\psarc(13.7,0){0.7}{140}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}&\psset{unit=0.5cm}
\begin{pspicture}(-0.3,-0.75)(14,3.5)
%\psgrid
\psaxes[linewidth=1.25pt,Dx=20,Dy=10](0,0)(-0.3,-0.5)(14,3)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}
\psline(0,0)(10.4,2.8)
\psline(13.7,0)(12,2.9)
\psarc(0,0){1}{0}{20}\rput(2,0.25){\footnotesize $d$}
\psarc(13.7,0){1}{120}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/50.png)
- Première modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et 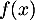 la hauteur correspondante de la balle.
la hauteur correspondante de la balle.
Selon ce modèle :- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
- Vérifier que
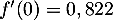 .
.
- Donner une mesure en degré de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
- Quelle propriété graphique de la courbe
 permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
- Seconde modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
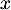 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et  la hauteur correspondante de la balle.
Selon ce modèle :
la hauteur correspondante de la balle.
Selon ce modèle :
- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On précise que
 et
et 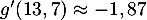 .
.
- Donner une mesure en degré de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
- Justifier que
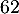 est une valeur approchée, arrondie à l'unité près, d'une mesure en degré de l'angle d'atterrissage de la balle.
est une valeur approchée, arrondie à l'unité près, d'une mesure en degré de l'angle d'atterrissage de la balle.
Tableau : extrait d'une feuille de calcul donnant une mesure en degré d'un angle quand on connait sa tangente :
![\[%\begin{tabularx}{\linewidth}{|c|*{13}{>{\centering \arraybackslash}X|}}
\begin{tabular}{|c|p{2em}|*{12}{c|}}
\hline
&A&B&C&D&E&F&G&H&I&J&K&L&M\\ \hline
1&$\!\!\tan(\theta)$&0,815&0,816&0,817&0,818&0,819&0,82&0,821&0,822&0,823&0,824&0,825&0,826\\ \hline
2&\scriptsize \mbox{$\theta$ en} degr\'es&39,18&39,21&39,25&39,28&39,32&39,35&39,39&39,42&39,45&39,49&39,52&39,56\\ \hline
3& &&&&&&&&&&&&\\ \hline
4&$\!\!\tan(\theta)$&0,285& 0,286& 0,287& 0,288& 0,289&0,29&0,291&0,292&
0,293&0,294&0,295 &0,296\\ \hline
5&\scriptsize \mbox{$\theta$ en} degr\'es&15,91 &15,96&16,01& 16,07& 16,12& 16,17& 16,23& 16,28& 16,33& 16,38& 16,44& 16,49\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/60.png)
- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On précise que
Partie C : interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants:
![\[\begin{tabular}{|*4{p{4.2cm}|}}\hline
Angle de d\'ecollage en degr\'e
&Hauteur maximale en yard
&Angle d'atterrissage en degr\'e
&Distance horizontale en yard au point de chute\\ \hline
24&32&52&137\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/61.png)
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée. Partie A : études de deux fonctions
On considère les deux fonctions
On admet que les fonctions
- On donne le tableau de variations complet de la fonction
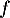 sur l'intervalle
sur l'intervalle  .
.
{$x$} \uput[u](1.6,1.4){$0$} \uput[u](4,1.4){$6,85$} \uput[u](6,1.4){$+ \infty$}
\rput(0.75,0.75){$f(x)$}\uput[u](1.65,0){$0$}\uput[d](4,1.5){$f(6,85)$}\uput[u](6,0){$- \infty$}
\psline{->}(1.9,0.4)(3.2,1.1)\psline{->}(4.8,1.1)(5.7,0.4)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/72.png)
- Justifier la limite de
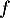 en
en  .
.
- Justifier les variations de la fonction
 .
.
- Résoudre l'équation
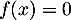 .
.
- Justifier la limite de
-
- Déterminer la limite de
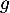 en
en  .
.
- Démontrer que, pour tout réel
 appartenant à
appartenant à  on a :
on a :  .
.
- Étudier les variations de la fonction
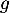 et dresser son tableau de variations sur
et dresser son tableau de variations sur 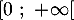 .
.
Préciser une valeur approchée à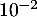 près du maximum de
près du maximum de  .
.
- Montrer que l'équation
 admet une unique solution non nulle et déterminer, à
admet une unique solution non nulle et déterminer, à  près, une valeur approchée de cette solution.
près, une valeur approchée de cette solution.
- Déterminer la limite de
Partie B : trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club» de golf.
On souhaite exploiter les fonctions
On admettra ici que
On donne ci-dessous les représentations graphiques de
![$$(-1,-1)(14,3.5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.2pt]
\psaxes[linewidth=1.25pt,Dx=20,Dy=20]{->}(0,0)(-1,-1)(14,3.5)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}\uput[ur](12,2.2){\blue $\mathcal{C}_g$}
\uput[dl](0,0){0}\uput[d](1,0){1}\uput[l](0,1){1}\uput[d](13.7,0){13,7}
$$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/95.png)
Pour
On appelle « angle de décollage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (
De même, on appelle « angle d'atterrissage » de la balle, l'angle entre l'axe des abscisses et la tangente à la courbe (
Tous les angles sont mesurés en degré.
(-0.3,-0.3)(14,3)
\psplot[plotpoints=1000]{0}{2}{0.822 x mul}
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=red]{0}{13.7}{13.7 x mul x dup mul sub 0.06 mul}\uput[ul](3,2){\red $\mathcal{C}_f$}
\psline(13.7,0)(11,2)
\psarc(0,0){0.7}{0}{40}\rput(1.2,0.5){\footnotesize $d$}
\psarc(13.7,0){0.7}{140}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}&\psset{unit=0.5cm}
\begin{pspicture}(-0.3,-0.75)(14,3.5)
%\psgrid
\psaxes[linewidth=1.25pt,Dx=20,Dy=10](0,0)(-0.3,-0.5)(14,3)
\psplot[plotpoints=1000,linewidth=1.25pt,linecolor=blue]{0}{13.7}{2.2 0.15 x mul sub 2.71828 0.2 x mul exp mul 2.2 sub}
\psline(0,0)(10.4,2.8)
\psline(13.7,0)(12,2.9)
\psarc(0,0){1}{0}{20}\rput(2,0.25){\footnotesize $d$}
\psarc(13.7,0){1}{120}{180}\rput(12.4,0.5){\footnotesize $a$}
\uput[d](13.7,0){\footnotesize 13,7}
\end{pspicture}\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/111.png)
- Première modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et  la hauteur correspondante de la balle.
la hauteur correspondante de la balle.
Selon ce modèle :- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
- Vérifier que
 .
.
- Donner une mesure en degré de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
- Quelle propriété graphique de la courbe
 permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
- Seconde modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
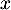 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et 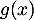 la hauteur correspondante de la balle.
Selon ce modèle :
la hauteur correspondante de la balle.
Selon ce modèle :
- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On précise que
 et
et 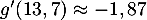 .
.
- Donner une mesure en degré de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
- Justifier que
 est une valeur approchée, arrondie à l'unité près, d'une mesure en degré de l'angle d'atterrissage de la balle.
est une valeur approchée, arrondie à l'unité près, d'une mesure en degré de l'angle d'atterrissage de la balle.
Tableau : extrait d'une feuille de calcul donnant une mesure en degré d'un angle quand on connait sa tangente :
![\[%\begin{tabularx}{\linewidth}{|c|*{13}{>{\centering \arraybackslash}X|}}
\begin{tabular}{|c|p{2em}|*{12}{c|}}
\hline
&A&B&C&D&E&F&G&H&I&J&K&L&M\\ \hline
1&$\!\!\tan(\theta)$&0,815&0,816&0,817&0,818&0,819&0,82&0,821&0,822&0,823&0,824&0,825&0,826\\ \hline
2&\scriptsize \mbox{$\theta$ en} degr\'es&39,18&39,21&39,25&39,28&39,32&39,35&39,39&39,42&39,45&39,49&39,52&39,56\\ \hline
3& &&&&&&&&&&&&\\ \hline
4&$\!\!\tan(\theta)$&0,285& 0,286& 0,287& 0,288& 0,289&0,29&0,291&0,292&
0,293&0,294&0,295 &0,296\\ \hline
5&\scriptsize \mbox{$\theta$ en} degr\'es&15,91 &15,96&16,01& 16,07& 16,12& 16,17& 16,23& 16,28& 16,33& 16,38& 16,44& 16,49\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/121.png)
- Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On précise que
Partie C : interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants:
![\[\begin{tabular}{|*4{p{4.2cm}|}}\hline
Angle de d\'ecollage en degr\'e
&Hauteur maximale en yard
&Angle d'atterrissage en degr\'e
&Distance horizontale en yard au point de chute\\ \hline
24&32&52&137\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022/122.png)
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée.
Correction exercice 4
Partie A : études de deux fonctions
Partie B : trajectoires d'une balle de golf
Partie C : interrogation des modèles
Les angles de décollage et d'atterissage sont très clairement différents, et le modèle parabolique de la fonction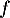 n'est donc clairement pas adapté.
n'est donc clairement pas adapté.
La hauteur maximale est aussi mieux approchée par le second modèle.
Parmi les deux modèles étudiés, le modèle fourni par la fonction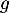 semble donc
le plus adapté.
semble donc
le plus adapté.
Cacher la correction
Partie A : études de deux fonctions
-
- On a, pour tout
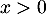 ,
,
![\[f(x)=-0,06x^2\lp1-\dfrac{13,7}x\rp\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/2.png)
avec
![\[\lim_{x\to+\infty}-0,06x^2=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/3.png)
et
![\[\lim_{x\to+\infty}\lp1-\dfrac{13,7}x\rp=1\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/4.png)
d'où, par produit, la limite
![\[\lim_{x\to+\infty}f(x)=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/5.png)
- On a
 d'où le tableau de signes et de variations
d'où le tableau de signes et de variations
![\[\begin{tabular}{|c|*5c|}\hline
$x$ & 0 && 6,85 && $+\infty$ \\\hline
$-2x+13,7$&& $+$ &\zb&$-$&\\\hline
$f'(x)$&& $+$ &\zb&$-$&\\\hline
&&&$f(6,85)$&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/7.png)
- On a
![\[\begin{array}{ll}f(x) = 0&\iff -x^2+13,7x=0\\
&\iff x(-x+13,7)=0\\
&\iff x=0 \text{ ou } x=13,7\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/8.png)
- On a, pour tout
-
- On a
![\[\lim_{x\to+\infty}(-0,15x+2,2)=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/9.png)
et
![\[\lim_{x\to+\infty}e^{0,2x}=+\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/10.png)
et donc, par produit,
![\[\lim_{x\to+\infty}(-0,15x+2,2)e^{0,2x}=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/11.png)
et donc aussi,
![\[\lim_{x\to+\infty}g(x)=-\infty\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/12.png)
- On a
 avec
avec
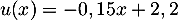 et
et  et
et 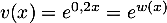 donc
donc
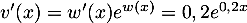 .
.
On obtient donc , soit pour tout
, soit pour tout  ,
,
![\[\begin{array}{ll}g'(x)&=-0,15e^{0,2x}+(-0,15x+2,2)\tm0,2e^{0,2x}\\
&=\Bigl(-0,15+0,2(-0,15x+2,2)\Bigr)e^{0,2x}\\
&=\lp-0,03x+0,29\right) e^{0,2x}
\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/20.png)
- On obtient alors le tableau de signes et de variations:
![\[\begin{tabular}{|c|*5c|}\hline
$x$ & 0 && $29/3$ && $+\infty$ \\\hline
$-0,03x+0,29$&& $+$ &\zb&$-$&\\\hline
$e^{0,2x}$&& $+$ &\vline&$+$&\\\hline
$g'(x)$&& $+$ &\zb&$-$&\\\hline
&&&$g\lp29/3\rp$&&\\
$g$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&0&&&&$-\infty$\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/21.png)
On trouve comme valeur maximale
![\[g\lp\dfrac{29}3\rp\simeq2,98\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/22.png)
- on a pour tout
![$x\in]0;29/3]$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/23.png) ,
, 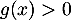 et donc l'équation
et donc l'équation 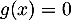 n'admet aucune soltuion.
n'admet aucune soltuion.
Sur , la fonction
, la fonction 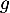 est continue (car même dérivable),
strictement décroissante
avec
est continue (car même dérivable),
strictement décroissante
avec  et
et
 .
.
Ainsi, d'après le théorème des valeurs intermédiaires, ou théorème de la bijection, l'équation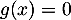 admet une unique solution sur
admet une unique solution sur 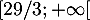 .
.
Finalement, l'équation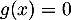 admet une unique solution sur
admet une unique solution sur ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/33.png) , c'est-à-dire une unique solution non nulle.
, c'est-à-dire une unique solution non nulle.
Avec la calculatrice, par balayage ou dichotomie par exemple, on trouve comme valeur approchée de cette solution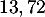 .
.
- On a
Partie B : trajectoires d'une balle de golf
- Première modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards,
 représente la distance horizontale parcourue par la balle après la frappe et
représente la distance horizontale parcourue par la balle après la frappe et 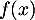 la hauteur correspondante de la balle.
la hauteur correspondante de la balle.
Selon ce modèle :- On a vu que le maximum de
 est
est 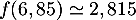 soit une hauteur maximale de 28,15 yards.
soit une hauteur maximale de 28,15 yards.
- On a
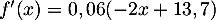 ,
d'où
,
d'où  .
.
-
 est le coefficient directeur de la tangente à la courbe de
est le coefficient directeur de la tangente à la courbe de 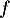 en 0,
c'est-à-dire justement au décollage.
en 0,
c'est-à-dire justement au décollage.
On a donc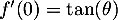 et donc, d'après le tableau donné dans
l'énoncé,
et donc, d'après le tableau donné dans
l'énoncé, 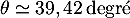 .
.
- La courbe est une parabole. En particulier, elle est symétrique par rapport à la droite
 , abscisse de son sommet.
Les points de décollage
, abscisse de son sommet.
Les points de décollage  et d'atterissage
et d'atterissage 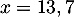 sont symétriques eux aussi par rapport à cette droite, et il en est donc de même des angles
que forment les tangentes à la courbes en ces deux points,
c'est-à-dire que les angles de décollage et d'atterrissage de la balle sont
égaux.
sont symétriques eux aussi par rapport à cette droite, et il en est donc de même des angles
que forment les tangentes à la courbes en ces deux points,
c'est-à-dire que les angles de décollage et d'atterrissage de la balle sont
égaux.
- On a vu que le maximum de
- Seconde modélisation
- D'après ce modèle, la hauteur maximale est
![\[g\lp\dfrac{29}3\rp\simeq2,98\]](/Generateur-Devoirs/TS/ChapExponentielle/ex12052022_c/48.png)
soit 29,8 yard. On précise que et .
.
-
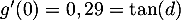 soit, d'après le tableau foruni,
soit, d'après le tableau foruni, 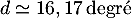 .
.
- De même pour l'angle d'atterissage,
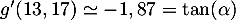 soit
soit 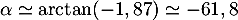 soit,
arrondie à l'unité près, environ 62 degrés.
soit,
arrondie à l'unité près, environ 62 degrés.
- D'après ce modèle, la hauteur maximale est
Partie C : interrogation des modèles
Les angles de décollage et d'atterissage sont très clairement différents, et le modèle parabolique de la fonction
La hauteur maximale est aussi mieux approchée par le second modèle.
Parmi les deux modèles étudiés, le modèle fourni par la fonction
Cacher la correction
Voir aussi: