Oral du bac: suite et géométrie dans l'espace
géométrie dans l'espace, suites récurrentes
- L'utilisation d'une calculatrice est autorisée.
- La qualité des raisonnements, de l'expression, et la précision des justifications prendront une part importante dans l'appréciation de l'interrogation orale.
- Il s'agit d'une épreuve orale: il n'est pas indispensable de rédiger l'ensemble des réponses, des calculs, du raisonnement …
Par contre vous devez être en mesure d'apporter toutes les justifications nécessaires.
L'exposé de la méthode et du raisonnement sera pris en compte.
Exercice 1: Géométrie dans un cube
On considère le cube  de côté 1,
de côté 1, 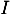 est le milieu de
est le milieu de ![$[EF]$](/Generateur-Devoirs/TS/ChapGeomSpace/exOralCube/3.png) et
et 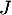 le symétrique de
le symétrique de 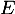 par rapport à
par rapport à 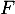 .
.
L'espace est rapporté au repère orthonormé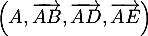 .
.

\psline(4,0.5)(4,3.5)
\psline(4,3.5)(1,3.5)
\psline(0,3)(1,3.5)
\psline(3,3)(4,3.5)
\psline[linestyle=dashed](1,0.5)(4,0.5)
\psline[linestyle=dashed](3,0)(4,.5)
\psline[linestyle=dashed](1,0.5)(1,3.5)
\rput(-0.2,-0.2){$A$}
\rput(3.2,-0.2){$B$}
\rput(4.3,0.6){$C$}
\rput(1.2,0.7){$D$}
\rput(-.2,3){$E$}
\rput(2.95,3.2){$F$}
\rput(4.3,3.7){$G$}
\rput(.7,3.7){$H$}
\rput(1.5,2.98){$\tm$}\rput(1.5,2.65){$I$}
\psline[linewidth=.5pt](3,3)(6,3)
\rput(6,2.98){$\tm$}\rput(5.9,2.65){$J$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exOralCube/8.png)
L'espace est rapporté au repère orthonormé

\psline(4,0.5)(4,3.5)
\psline(4,3.5)(1,3.5)
\psline(0,3)(1,3.5)
\psline(3,3)(4,3.5)
\psline[linestyle=dashed](1,0.5)(4,0.5)
\psline[linestyle=dashed](3,0)(4,.5)
\psline[linestyle=dashed](1,0.5)(1,3.5)
\rput(-0.2,-0.2){$A$}
\rput(3.2,-0.2){$B$}
\rput(4.3,0.6){$C$}
\rput(1.2,0.7){$D$}
\rput(-.2,3){$E$}
\rput(2.95,3.2){$F$}
\rput(4.3,3.7){$G$}
\rput(.7,3.7){$H$}
\rput(1.5,2.98){$\tm$}\rput(1.5,2.65){$I$}
\psline[linewidth=.5pt](3,3)(6,3)
\rput(6,2.98){$\tm$}\rput(5.9,2.65){$J$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exOralCube/8.png)
- Par lecture graphique, donner les coordonnées de
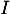 et
et 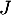 .
.
- En déduire les coordonnées des vecteurs
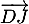 ,
, 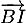 et
et 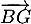 .
.
- Montrer que
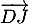 est un vecteur normal au plan
est un vecteur normal au plan 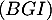 .
.
- Montrer qu'une équation cartésienne du plan
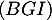 est
est
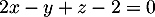 .
.
Correction exercice 1
Cacher la correction
- Par lecture graphique,
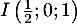 et
et 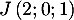 .
.
- On en déduit
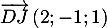 ,
,
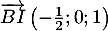 et
et
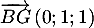 .
.
-
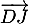 est normal au plan
est normal au plan 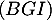 si et seulement si il est orthogonal à deux vecteurs non colinéaires du plan, par exemple
si et seulement si il est orthogonal à deux vecteurs non colinéaires du plan, par exemple
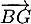 et
et 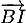 , ce qui est bien le cas car:
, ce qui est bien le cas car:
![\[\overrightarrow{DJ}\cdot\overrightarrow{BG}=2\tm0+(-1)\tm1+1\tm1=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/exOralCube_c/10.png)
et
![\[\overrightarrow{DJ}\cdot\overrightarrow{BI}=2\tm\lp-\dfrac12\rp+(-1)\tm0+1\tm1=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/exOralCube_c/11.png)
- Un vecteur normal au plan
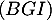 est donc
est donc 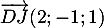 et donc ce plan a une équation cartésienne de la forme
et donc ce plan a une équation cartésienne de la forme
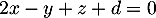 .
.
De plus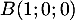 appartient à ce plan, d'où
appartient à ce plan, d'où
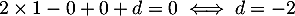 .
.
Une équation cartésienne du plan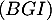 est donc bien
est donc bien
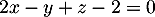 .
.
Cacher la correction
Exercice 2: Suite récurrente et suite auxiliaire géométrique avec logarithme
On considère la suite 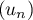 définie par
définie par 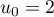 et,
pour tout entier
et,
pour tout entier 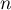 ,
, 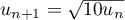 .
.
On note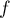 la fonction définie par l'expression
la fonction définie par l'expression
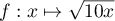 .
.
On note
- Tracer l'allure de la courbe représentative de la fonction
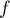 et construire sur l'axe des abscisses les premiers termes
et construire sur l'axe des abscisses les premiers termes 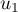 ,
,
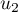 , … de la suite
, … de la suite 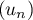 .
.
Quelles conjectures peut-on faire ? - On pose
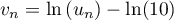 .
Montrer que
.
Montrer que 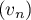 est une suite géométrique.
est une suite géométrique.
En déduire les expressions de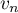 , puis de
, puis de 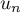 en fonction de
en fonction de 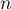 .
.
- En déduire que la limite de la suite
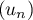 .
.
Correction exercice 2
Cacher la correction
-
![\psset{unit=0.8cm,arrowsize=7pt}
\begin{pspicture}(-1,-1)(12,12)
\psline{->}(-.5,0)(12,0)
\psline{->}(0,-.5)(0,12)
\newcommand{\f}[1]{10 #1 mul 0.5 exp}
\psplot{0}{10}{\f{x}}
\psplot[linewidth=1.4pt]{0}{12}{\f{x}}
\rput(11.6,10.3){$\mathcal{C}_f$}
\psplot{-0.2}{12}{x}\rput(11.5,12){$y=x$}
\newcommand\fn[2]{%
\ifnum#1=1
\f{#2}%
\else
\f{\fn{\numexpr#1-1}{#2}}%
\fi
}
\def\xinit{2}
\def\nmax{4}
\psline[linestyle=dashed](\xinit,0)(!\xinit\space\f{\xinit})(!\f{\xinit}\space\f{\xinit})
\rput(\xinit,-0.3){$u_0=2$}
\multido{\i=1+1}{\nmax}{
\psline[linestyle=dashed](!\fn{\i}{\xinit} \space 0)(!\fn{\i}{\xinit} \space \fn{\i}{\xinit})(!\fn{\i}{\xinit} \space \fn{\numexpr\i+1}{\xinit})(!\fn{\numexpr\i+1}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
\rput(!\fn{\i}{\xinit}\space 0){$\tm$}
\rput(!\fn{\i}{\xinit}\space -0.3){$u_\i$}
}
\def\ninf{20}
\psline[linecolor=blue](!\fn{\ninf}{\xinit}\space 0)(!\fn{\numexpr\ninf+1}{\xinit}\space\fn{\numexpr\ninf+1}{\xinit})(!0\space\fn{\numexpr\ninf+1}{\xinit})
\rput(!\fn{\ninf}{\xinit}\space -0.3){\blue$\ell$}
\rput(!-.3\space\fn{\ninf}{\xinit}){\blue$\ell$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapSuites/exOral02_c/1.png)
On peut conjecturer que la suite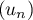 est strictement croissante,
minorée par
est strictement croissante,
minorée par 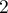 , majorée par
, majorée par 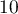 , et convergente vers une limite
, et convergente vers une limite 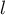 .
.
-
![\begin{array}{ll}
v_{n+1}&=\ln\left( u_{n+1}\rp-\ln(10)\\[0.4cm]
&=\ln\left( \sqrt{10u_n}\rp-\ln(10)\\[0.4cm]
&=\dfrac12\ln(10u_n)-\ln(10)\\[0.4cm]
&=\dfrac12\Bigl(\ln(10)+\ln\left( u_n\rp\Bigr)-\ln(10)\\[0.4cm]
&=\dfrac12\ln\left( u_n\rp-\dfrac12\ln(10) \\[0.4cm]
&=\dfrac12\lp\ln\lp u_n\rp-\ln(10)\rp=\dfrac12 v_n
\enar](/Generateur-Devoirs/TS/ChapSuites/exOral02_c/6.png)
Ainsi, la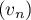 est géométrique de raison
est géométrique de raison  .
.
On en déduit que, pour tout entier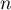 ,
,
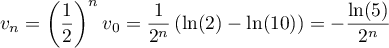 ,
et donc, que
,
et donc, que
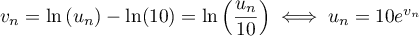 .
.
- Comme
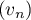 est une suite géométrique de raison
est une suite géométrique de raison
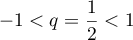 , on a
, on a 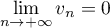 , et alors, par
composition des limites,
, et alors, par
composition des limites,
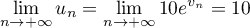 .
.
Cacher la correction
Voir aussi: