Oral de Bac - Logarithme et exponentielles - Limites et asymptote oblique

Exercice corrigé - Spécialité maths, terminale générale

Soit 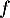$f$ la fonction définie par l'expression $f(x)=\ln\left( e^x+e^{-x}\rp$.
On note $\mathcal{C}$ sa courbe dans un repère du plan.
  1. Quel est l'ensemble de définition de $f$ ?
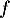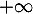  2. Etudier la limite de $f$ en $+\infty$.
  3. Montrer que, pour tout réel $x$, $f(x)=x+\ln\lp1+e^{-2x}\rp$.
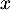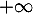  4. Résoudre l'équation $f(x)=x+2$ en $+\infty$.

Correction
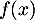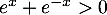  1. Le logarithme est défini sur $\R_+^*=]0;+\infty[$. $f(x)$ est ainsi défini pour les valeurs réelles de $x$ telles que $e^x+e^{-x}>0$.
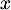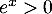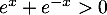    Or pour tout réel $x$, $e^x>0$ et $e^{-x}>0$, donc $e^x+e^{-x}>0$.
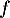    $f$ est ainsi définie sur $\R$.
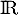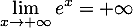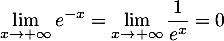  2. $\dsp\lim_{x\to+\infty} e^x=+\infty$ et $\dsp\lim_{x\to+\infty}e^{-x}=\lim_{x\to+\infty}\dfrac{1}{e^x}=0$.
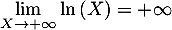    Ainsi, par somme des limites, $\dsp\lim_{x\to+\infty}e^x+e^{-x}=+\infty$, et, comme $\dsp\lim_{X\to+\infty}\ln\left( X\rp=+\infty$, par composition des limites, $\dsp\lim_{x\to+\infty}\ln\left( e^x+e^{-x}\rp=\lim_{X\to+\infty}\ln(X)=+\infty$.
  3. Pour tout réel $x$,
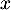    \[f(x)=\ln\left( e^x+e^{-x}\rp=\ln\left( e^x\left( 1+e^{-2x}\rp\rp=\ln\left( e^x\rp+\ln\left( 1+e^{-2x}\rp=x+\ln\left( 1+e^{-2x}\rp\]


  4. \[\begin{array}{ll} f(x)=x+2&\iff x+\ln\lp1+e^{-2x}\rp=x+2\\[.5em] &\iff\ln\lp1+e^{-2x}\rp=2\\[.5em] &\iff 1+e^{-2x}=e^2\\[.5em] &\iff e^{-2x}=e^2-1\\[.5em] &\iff -2x=\ln\left( e^2-1\rp\\[.5em] &\iff x=-\dfrac12\ln\left( e^2-1\rp\enar\]




Cacher la correction


Tags:LogarithmeExponentielle

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 1 - h3: 0