Limites, asymptotes, variation
Exercice corrigé - Spécialité maths, terminale générale
On note
- Déterminer les limites de
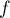 en
en 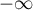 et
et 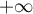 .
.
- Déterminer les limites de
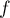 en
en 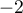 et
et 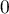 .
.
- Interpréter graphiquement les résultats des deux questions précédentes.
- Calculer
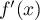 et dresser le tableau de variation de
et dresser le tableau de variation de 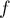 .
.
- Tracer dans un repère les asymptotes de
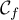 et
l'allure de
et
l'allure de 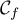 .
.
Correction
 est la fonction définie sur
est la fonction définie sur  par
par
 .
.
Cacher la correction
- Pour tout
 ,
,
 .
.
On a et
et
 ,
et donc, par quotient des limites,
,
et donc, par quotient des limites,
 .
.
De même, .
.
- Limite en
 :
:
 .
.
Le dénominateur tend quant à lui vers (
( est une valeur
interdite).
Il nous faut de plus déterminer le signe de celui-ci.
est une valeur
interdite).
Il nous faut de plus déterminer le signe de celui-ci.
 est un trinôme du second degré qui admet comme
racines
est un trinôme du second degré qui admet comme
racines  et
et  , et qui a donc pour signes
, et qui a donc pour signes

Ainsi, (c'est-à-dire que
(c'est-à-dire que  ),
),
puis, par quotient des limites,
De même, (c'est-à-dire que
(c'est-à-dire que  ),
),
puis, par quotient des limites,
Limites en :
:
 .
.
De même que précédemment, en utilisant le signe du dénominateur ,
on obtient:
,
on obtient:
 et
et
 .
.
- On en déduit que la droite d'équation
 est une asymptote
horizontale à
est une asymptote
horizontale à  en
en  et
et  ,
et que les droites d'équation
,
et que les droites d'équation  et
et  sont des asymptotes
verticales à
sont des asymptotes
verticales à  .
.
-
 .
.

-
On peut alors tracer la courbe représentant  en commençant
par ses asymptotes.
en commençant
par ses asymptotes.
On n'oublie pas non plus que admet une tangente
horizontale en
admet une tangente
horizontale en  .
.

Cacher la correction
Tags:Limites de fonctionsFonctions
Voir aussi:
