Étude complète de fonction

Exercice corrigé - Spécialité maths, terminale générale

est la fonction définie sur $\R$ par l'expression:

.
Dresser le tableau de variation de

. Préciser les limites de

en $-\infty$ et $+\infty$ .

Correction
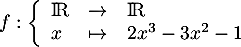
$f:\la\begin{array}{lcl}\R&\to&\R\\x&\mapsto&2x^3-3x^2-1\enar\right.$

La dérivée de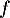

est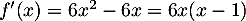

qui est un trinôme du second degré dont les racines (évidentes une fois factorisé) sont 0 et 1, et on a donc le tableau de signes et de variations:

$\begin{tabular}{|c|lcccccr|}\hline $x$ &$-\infty$ &&0&&1&&$+\infty$\\\hline $f'(x)$ && $+$ &0&$-$&0&$+$&\\\hline &&&$-1$&&&&$+\infty$\\ $f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\ &$-\infty$&&&&$-4$&&\\\hline \end{tabular}$

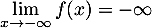En $-\infty$ , on a $\dsp\lim_{x\to-\infty}2x^3=\lim_{x\to-\infty}-3x^2=-\infty$ , et donc, par somme des limites, on obtient $\dsp\lim_{x\to-\infty}f(x)=-\infty$ .

En $+\infty$ , on a une forme indéterminée " $\infty-\infty$ ". On factorise donc

$f(x)=2x^3\lp1-\dfrac3{2x}-\dfrac1{2x^3}\rp$

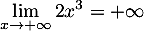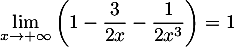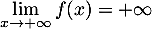avec $\dsp\lim_{x\to+\infty}2x^3=+\infty$ et $\dsp\lim_{x\to+\infty}\lp1-\dfrac3{2x}-\dfrac1{2x^3}\rp=1$ , et donc, par produit des limites, $\dsp\lim_{x\to+\infty}f(x)=+\infty$ .

Cacher la correction

Tags:Limites de fonctions Fonctions

Autres sujets au hasard:

Voir aussi:

Quelques devoirs

Devoir corrigé

Suites et fonctions - Sujet A

sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique

Devoir corrigé

Suites et fonctions - Sujet B

Devoir corrigé

Suites et fonctions - Sujet A

Devoir corrigé

Suites et fonctions - Sujet B

Devoir corrigé

Suites et fonctions

maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe