Deux équations avec logarithme

Exercice corrigé - Spécialité maths, terminale générale

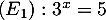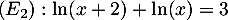
Résoudre les équations: $(E_1): 3^x=5$    et    $(E_2): \ln(x+2)+\ln(x)=3$

Correction
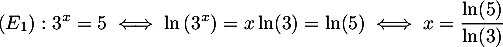$(E_1): 3^x=5 \iff \ln\lp3^x\rp=x\ln(3)=\ln(5)\iff x=\dfrac{\ln(5)}{\ln(3)}$.

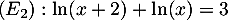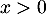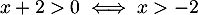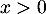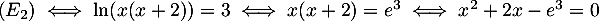
$(E_2): \ln(x+2)+\ln(x)=3$ Les expressions sont définies pour $x>0$ et $x+2>0\iff x>-2$, donc $x>0$. $(E_2)\iff \ln(x(x+2))=3\iff x(x+2)=e^3\iff x^2+2x-e^3=0$

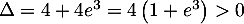$\Delta=4+4e^3=4\lp1+e^3\rp>0$ et l'équation admet donc deux solutions

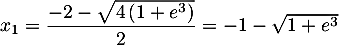$x_1=\dfrac{-2-\sqrt{4\lp1+e^3\right)}}2=-1-\sqrt{1+e^3}$
et
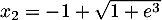$x_2=-1+\sqrt{1+e^3}$.

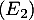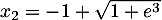Comme $x_1<0$, l'équation $(E_2)$ admet donc pour unique solution $x_2=-1+\sqrt{1+e^3}$.

Cacher la correction


Tag:Logarithme

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 1 - h3: 0