Bac 2021 (sujet 0): QCM, suite et fonctions
Exercice corrigé - Spécialité maths, terminale générale
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Une réponse exacte rapporte un point.
Une réponse fausse, une réponse multiple ou l’absence de réponse à une question ne rapporte ni n’enlève de point. Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie. Aucune justification n’est demandée.
Une réponse fausse, une réponse multiple ou l’absence de réponse à une question ne rapporte ni n’enlève de point. Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie. Aucune justification n’est demandée.
- On considère les suites
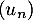 et
et 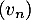 telles que, pour tout entier naturel
telles que, pour tout entier naturel 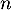 ,
,
![\[u_n= 1-\left(\frac{1}{4}\right)^n \hspace{3em} \text{et }\hspace{3em} v_n=1+\left(\frac{1}{4}\right)^n.\]](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0/4.png)
On considère de plus une suite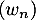 qui, pour tout entier naturel
qui, pour tout entier naturel 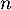 , vérifie
, vérifie 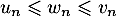 .
.
On peut affirmer que :
a. Les suites et
et 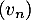 sont géométriques.
sont géométriques.
b. La suite converge vers 1.
converge vers 1.
c. La suite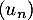 est minorée par 1.
est minorée par 1.
d. La suite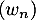 est croissante.
est croissante.
- On considère la fonction
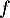 définie sur
définie sur 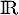 par :
par : 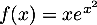 .
.
La fonction dérivée de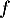 est la fonction
est la fonction 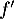 définie sur
définie sur  par :
par :
a.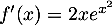
b.
c.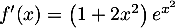
d.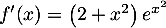 .
.
- Que vaut
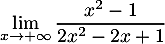 ?
?
a.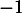
b.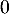
c.
d. .
.
- On considère une fonction
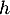 continue sur l’intervalle
continue sur l’intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0/29.png) telle que
telle que
![\[h(-1)=0 \qquad h(0)=2\qquad h(1)=0 .\]](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0/30.png)
On peut affirmer que :
- La fonction
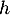 est croissante sur l’intervalle
est croissante sur l’intervalle ![$[-1~;~0]$](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0/32.png) .
.
- La fonction
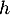 est positive sur l’intervalle
est positive sur l’intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0/34.png) .
.
- Il existe au moins un nombre réel
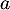 dans l’intervalle [0 ; 1] tel que
dans l’intervalle [0 ; 1] tel que 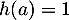 .
.
- L’équation
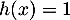 admet exactement deux solutions dans l’intervalle
admet exactement deux solutions dans l’intervalle ![$[-1~;~1]$](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0/38.png) .
.
- La fonction
- On suppose que
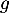 est une fonction dérivable sur l’intervalle
est une fonction dérivable sur l’intervalle ![$[-4~;~4]$](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0/40.png) .
On donne ci-contre la représentation graphique de sa fonction dérivée
.
On donne ci-contre la représentation graphique de sa fonction dérivée  .
.
On peut affirmer que :-
 admet un maximum en
admet un maximum en 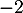 .
.
-
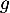 est croissante sur l’intervalle [1 ; 2].
est croissante sur l’intervalle [1 ; 2].
-
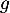 est convexe sur l’intervalle [1 ; 2].
est convexe sur l’intervalle [1 ; 2].
-
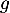 admet un minimum en 0.
admet un minimum en 0.
(\n,3.1)}
\multido{\n=-1+1}{5}{\psline[linewidth=0.25pt,linecolor=lightgray](-4.1,\n)(4.1,\n)}
\psaxes[linewidth=0.5pt]{->}(0,0)(-4.1,-1.2)(4.25,3.3)
%\pscurve[linewidth=0.4pt,linecolor=blue](-4,0)(-2,3)(0,0)(1,-1)(2,0)(3.5,2.8)(4,2)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=red]{-4}{0}{x x 4 add mul 0.75 mul neg}
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=red]{0}{2}{ x dup mul 1.75 mul x 3 exp 4 div sub x 2.5 mul sub}
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=red]{2}{4}{x 2 sub x 5 sub mul neg}
\psdots[dotstyle=Bullet,dotscale =1.1](-4,0)(-2,3)(0,0)(1,-1)(2,0)(4,2)
\uput[ul](-3,2.5){\red$\mathcal{C}_{g'}$}
%\psBspline[linewidth=1.3pt,linecolor=red]{B}(-4,0)(-3.2,2.2)(-2,3.4)(-1,2.2)(0,0)
%\psBspline[linewidth=1.3pt,linecolor=red]{B}(0,0)(0.4,-1)(1,-1.1)(1.6,-0.7)(2,0)
%\psBspline[linewidth=1.3pt,linecolor=red]{B}(2,0)(2.5,1.5)(3,2)(3.5,2.4)(4,2)
$$](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0/47.png)
-
Correction
Cacher la correction
- Réponse b.
Comme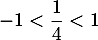 , on a
, on a
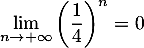 ,
et donc
,
et donc
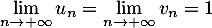 ,
et alors, d'après le théorème des gendarmes, on a aussi
,
et alors, d'après le théorème des gendarmes, on a aussi
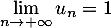
- Réponse c.
En dérivant le produit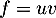 avc
avc 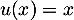 et
et 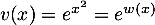 donc
donc 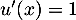 et
et 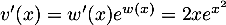 ,
on obtient alors
,
on obtient alors
![\[f'(x)= 1\times e^{x^2} + x \times 2x e^{x^2} = \lp1+2x^2\right) e^{x^2}\]](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0_c/10.png)
- Réponse c.
En factorisant par les termes de plus haut degré,
![\[\dfrac{x^2-1}{2x^2-2x+1}
=\dfrac{x^2\lp1-\frac1{x^2}\right)}{x^2\lp2-\frac2x+\frac1{x^2}\right)}
=\dfrac{1-\frac1{x^2}}{2-\frac2x+\frac1{x^2}}
\]](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0_c/11.png)
d'où la limite
![\[\lim_{x\to +\infty} \dfrac{x^2-1}{2x^2-2x+1}=\dfrac12\]](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0_c/12.png)
- Réponse c.
C'est une application du théorème des valeurs intermédiaires, sur l'intervalle![$[0;1]$](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0_c/13.png) sur lequel
la fonction est continue et telle que
sur lequel
la fonction est continue et telle que
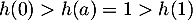 .
.
- Réponse c.
La fonction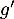 est croissante sur l'intervalle
est croissante sur l'intervalle ![$[1~;~2]$](/Generateur-Devoirs/TS/ChapFonctions/ex2021-s0_c/16.png) ,
donc la fonction
,
donc la fonction 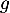 est convexe sur cet intervalle.
est convexe sur cet intervalle.
Cacher la correction
Tag:QCM
Voir aussi:
