Bac 2021 (15 mars, sujet 2): Distance point à un plan et volume d'une pyramide
Exercice corrigé - Spécialité maths, terminale générale
Dans l'espace rapporté à un repère orthonormé
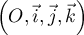 , on considère les points:
, on considère les points:
A de coordonnées (2 ; 0 ; 0), B de coordonnées (0 ; 3 ; 0) et C de coordonnées (0 ; 0 ; 1).
(2.4,4.5)(10.4,2)
%\psgrid
\psline(0,0)(8,0)(10.4,2)(10.4,4.5)(8,2.5)(8,0)
\psline(8,2.5)(0,2.5)(0,0)
\psline(0,2.5)(2.4,4.5)(10.4,4.5)
\psline[linestyle=dashed](0,0)(2.4,2)(2.4,4.5)
\psline[linestyle=dashed](2.4,2)(10.4,2)
\uput[dl](0,0){A}\uput[u](2.4,4.5){C}\uput[r](10.4,2){B}\uput[d](2.5,2){O}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321/2.png)
L'objectif de cet exercice est de calculer l'aire du triangle ABC.
A de coordonnées (2 ; 0 ; 0), B de coordonnées (0 ; 3 ; 0) et C de coordonnées (0 ; 0 ; 1).
(2.4,4.5)(10.4,2)
%\psgrid
\psline(0,0)(8,0)(10.4,2)(10.4,4.5)(8,2.5)(8,0)
\psline(8,2.5)(0,2.5)(0,0)
\psline(0,2.5)(2.4,4.5)(10.4,4.5)
\psline[linestyle=dashed](0,0)(2.4,2)(2.4,4.5)
\psline[linestyle=dashed](2.4,2)(10.4,2)
\uput[dl](0,0){A}\uput[u](2.4,4.5){C}\uput[r](10.4,2){B}\uput[d](2.5,2){O}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321/2.png)
L'objectif de cet exercice est de calculer l'aire du triangle ABC.
-
- Montrer que le vecteur
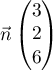 est normal au plan (ABC).
est normal au plan (ABC).
- En déduire qu'une équation cartésienne du plan (ABC) est :
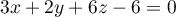 .
.
- Montrer que le vecteur
- On note
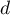 la droite passant par O et orthogonale au plan (ABC).
la droite passant par O et orthogonale au plan (ABC).
- Déterminer une représentation paramétrique de la droite
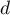 .
.
- Montrer que la droite
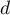 coupe le plan (ABC) au point H
de coordonnées
coupe le plan (ABC) au point H
de coordonnées
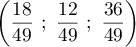 .
.
- Calculer la distance OH.
- Déterminer une représentation paramétrique de la droite
- On rappelle que le volume d'une pyramide est donné par:
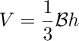 , où
, où  est l'aire d'une
base et
est l'aire d'une
base et  est la hauteur de la pyramide correspondant à cette base.
est la hauteur de la pyramide correspondant à cette base.
En calculant de deux façons différentes le volume de la pyramide OABC, déterminer l'aire du triangle ABC.
Correction
(Bac général, spécialité mathématiques, 15 mars 2021)
(2.4,4.5)(10.4,2)
%\psgrid
\psline(0,0)(8,0)(10.4,2)(10.4,4.5)(8,2.5)(8,0)
\psline(8,2.5)(0,2.5)(0,0)
\psline(0,2.5)(2.4,4.5)(10.4,4.5)
\psline[linestyle=dashed](0,0)(2.4,2)(2.4,4.5)
\psline[linestyle=dashed](2.4,2)(10.4,2)
\rput[l](-.4,-.5){A(2;0;0)}
\rput[l](2.4,4.8){C(0;0;1)}
\rput[l](10.6,2){B(0;3;0)}
\uput[d](2.5,2){O}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(1.2,1)
\rput(1.5,1.8){\red$\vec{i}$}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(4.9,2)
\rput(3.4,1.5){\red$\vec{j}$}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(2.4,4.5)
\rput(2,3){\red$\vec{j}$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/1.png)
Cacher la correction
(Bac général, spécialité mathématiques, 15 mars 2021)
(2.4,4.5)(10.4,2)
%\psgrid
\psline(0,0)(8,0)(10.4,2)(10.4,4.5)(8,2.5)(8,0)
\psline(8,2.5)(0,2.5)(0,0)
\psline(0,2.5)(2.4,4.5)(10.4,4.5)
\psline[linestyle=dashed](0,0)(2.4,2)(2.4,4.5)
\psline[linestyle=dashed](2.4,2)(10.4,2)
\rput[l](-.4,-.5){A(2;0;0)}
\rput[l](2.4,4.8){C(0;0;1)}
\rput[l](10.6,2){B(0;3;0)}
\uput[d](2.5,2){O}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(1.2,1)
\rput(1.5,1.8){\red$\vec{i}$}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(4.9,2)
\rput(3.4,1.5){\red$\vec{j}$}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(2.4,4.5)
\rput(2,3){\red$\vec{j}$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/1.png)
-
- Pour montrer que le vecteur
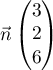 est normal au plan (ABC),
il suffit de démontrer que ce vecteur est orthogonal à deux vecteurs
directeurs du plan (ABC), par exemple
est normal au plan (ABC),
il suffit de démontrer que ce vecteur est orthogonal à deux vecteurs
directeurs du plan (ABC), par exemple  et
et 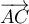 .
On a
.
On a 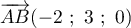 donc
donc
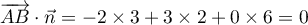 et ainsi
et ainsi 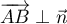 .
.
De même,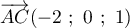 donc
donc
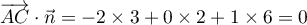 et ainsi, aussi,
et ainsi, aussi, 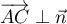 .
On en déduit que le vecteur
.
On en déduit que le vecteur 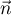 est normal au plan (ABC).
est normal au plan (ABC).
-
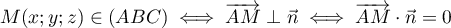 .
.
Or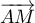 a pour coordonnées
a pour coordonnées 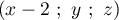 .
.
et donc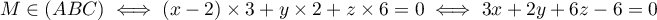
Le plan (ABC) a donc pour équation cartésienne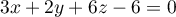 .
.
- Pour montrer que le vecteur
-
-
La droite
 est orthogonale au plan (ABC) donc elle a pour vecteur directeur le vecteur
est orthogonale au plan (ABC) donc elle a pour vecteur directeur le vecteur  normal à (ABC).
normal à (ABC).
De plus elle passe par le point O de coordonnées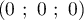 .
.
Une représentation paramétrique de la droite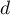 est donc
est donc
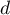
- La droite
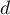 est orthogonale au plan (ABC),
et donc elle le coupe en un point H.
Soit
est orthogonale au plan (ABC),
et donc elle le coupe en un point H.
Soit 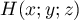 alors on a
alors on a
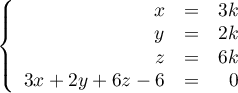
Donc, en substituant dans la troisième équation, on obtient
![\[\begin{array}{ll}&3\tm3k+2\tm 2k+6\tm 6k-6 = 0\\[.3em]
\iff& 9k+4k+36k=6\\
\iff& k=\dfrac{6}{49}\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/25.png)
On en déduit que
![\[\la\begin{array}{rcrcr}
x&=&3k&=&\dfrac{18}{49}\\[.8em]
y&=&2k&=&\dfrac{12}{49}\\[.8em]
z&=&6k&=&\dfrac{36}{49}\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/26.png)
et on a donc trouvé les coordonnées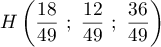 .
.
- On calcule alors directement
![\[\begin{array}{ll}
OH^2&=\left( x_{\text H}-x_{\text O}\rp^2 +
\left( y_{\text H}-y_{\text O}\rp^2 + \left( z_{\text H}-z_{\text O}\rp^2 \\[.6em]
&=\lp\dfrac{18}{49}\rp^2+\lp\dfrac{12}{49}\rp^2+\lp\dfrac{36}{49}\rp^2\\[1em]
&= \dfrac{18^2+12^2+36^2}{49^2} = \dfrac{1764}{49^2}
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/28.png)
On obtient donc la distance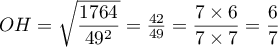 .
.
-
La droite
-
- On peut prendre le triangle OAB pour base de la pyramide OABC,
la hauteur est alors OC, et le volume
![\[\mathcal{V}=\dfrac{1}{3}\times \mathcal{B}\times OC\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/30.png)
avec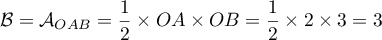 et
et 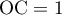 .
.
On obtient donc le volume
![\[\mathcal{V}=\dfrac{1}{3}\times 3 \times 1= 1\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/33.png)
- On peut aussi prendre le triangle ABC pour base de la pyramide OABC,
la hauteur est alors OH, et le volume est
![\[\mathcal{V}=\dfrac13\times \mathcal{B}'\times OH\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/34.png)
avec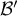 est l'aire du triangle ABC.
est l'aire du triangle ABC.
On a ici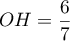 et
et 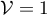 donc
donc
![\[\mathcal{V}=1=\dfrac13\times \mathcal{B}' \times \dfrac{6}{7}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/38.png)
d'où on déduit que
![\[\mathcal{B}'=\mathcal{A}_{ABC}==\dfrac{49}{14}= \dfrac72\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/39.png)
.
- On peut prendre le triangle OAB pour base de la pyramide OABC,
la hauteur est alors OC, et le volume
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie plane analytique, vecteurs et équations de droites, géométrie avec une hyperbole et ses tangentes, courbe représentative de la fonction inverse
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle - Analyse: étude d'une fonction: variations, limites, TVI, asymptotes, ...
étude de la convexité de fonctions (et variations, tangentes, limites, ...) et géométrie dans l'espace
