Bac 2016 (Amérique du nord) - Volume d'un récupérateur d'eau
Exercice corrigé - Spécialité maths, terminale générale
Un particulier veut faire fabriquer un récupérateur d'eau.
Ce récupérateur d'eau est une cuve qui doit respecter le cahier des
charges suivant:
Cette cuve est schématisée ci-contre.
![$$(-1.8,-0.5)(7,5)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\pspolygon(2,0)(2,1.8)(-1.3,2.5)(-1.3,0.7)
\rput(-3.3,0.7){\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}}
\psline(2.1,2.7)(5.4,2)
\psline(-1.3,2.5)(2.1,2.7)
\psline(2,1.8)(5.4,2)
\psline[linewidth=0.5pt](2,1.8)(2,3)\psline[linewidth=0.5pt](-1.3,2.5)(-1.3,3.7)
\psset{arrowsize=2pt 3}
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(2,3)(-1.3,3.7)
\psline[linewidth=0.5pt](2,1.8)(1.2,1.75)\psline[linewidth=0.5pt](2,0)(1.2,-0.05)
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(1.2,1.75)(1.2,-0.05)
\uput[l](1.2,0.85){2 m}\uput[u](1.35,3.35){5 m}
$$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/1.png)
La partie incurvée est modélisée par la courbe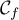 de la
fonction
de la
fonction 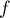 sur l'intervalle
sur l'intervalle ![$[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/4.png) définie par:
définie par:
![\[f(x)=x\ln \lp\dfrac{x}{2}\rp-x+2.\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/5.png)
La courbe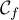 est représentée ci-dessous dans un repère
orthonormé d'unité 1m et constitue une vue de profil de la cuve.
est représentée ci-dessous dans un repère
orthonormé d'unité 1m et constitue une vue de profil de la cuve.
On considère les points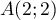 ,
, 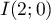 et
et 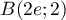 .
.
(-0.2,-0.25)(6,2.5)
\psaxes[linewidth=1.25pt](0,0)(0,0)(6,2.5)
\uput[u](2.8,0.2){$\mathcal{C}_f$}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\psframe[fillstyle=solid,fillcolor=lightgray](2,2)
\psdots(2,2)(5.437,2)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psplot[plotpoints=4000]{3}{5.8}{x 2 add 5.437 sub}
\uput[u](2,2){$A$}
\uput[u](5.437,2){$B$}
\uput[ul](5.75,2.2){$\mathcal{T}$}
\uput[dl](2,0){$I$}
\uput[dr](3.437,0){$D$}
\rput(1,1){Terrain}
\rput(3.2,1.2){Cuve}
\rput(4.7,0.5){Terrain}
\psline[linestyle=dotted,linewidth=1.5pt](2,2)(5.437,2)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/10.png)
Partie A L'objectif de cette partie est d'évaluer le volume de la cuve.
Partie B Pour tout réel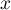 compris
entre
compris
entre 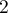 et
et 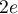 , on note
, on note 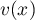 le volume d'eau, exprimé en m
le volume d'eau, exprimé en m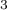 ,
se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est
égale à
,
se trouvant dans la cuve lorsque la hauteur d'eau dans la cuve est
égale à 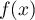 .
.
On admet que, pour tout réel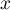 de l'intervalle [2 ; 2e],
de l'intervalle [2 ; 2e],
![\[v(x) = 5\left[\dfrac{x^2}{2}\ln \left( \dfrac{x}{2}\right) - 2x\ln\left( \dfrac{x}{2}\right) - \dfrac{x^2}{4} + 2x - 3\right].\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/49.png)
{\n}}
}
\pspolygon[fillstyle=solid,fillcolor=gray](2,0.1)(2,1.5)(0.35,2.3)(0.35,0.9)
\pspolygon[fillstyle=solid,fillcolor=gray](2,1.5)(0.35,2.3)(3.37,2.47)(5.08,1.7)
\pscustom[fillstyle=solid,fillcolor=gray]{
\pscurve(2,0.1)(3,0.316)(4,0.87)(5.08,1.75)
\psline(5.08,1.75)(2,1.5)
}
\pspolygon(5.437,2.1)(2,1.85)(0.35,2.7)(3.787,2.95)
\psline(2,1.85)(2,1.5)
\psline(0.35,2.7)(0.35,2.3)
\pscurve(0.35,0.9)(1.35,1.16)(2.35,1.72)(3.35,2.5)(3.787,2.95)
\psline[linestyle=dotted,linewidth=1.5pt](5.08,0.2)(5.08,1.75)(0,1.37)
\uput[d](5.2,0.3){$x$}
\uput[l](0,1.37){$f(x)$}
\multido{\n=0+1}{4}{\uput[l](0,\n){\n}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/50.png)
- elle doit être située à deux mètres de sa maison;
- la profondeur maximale doit être de deux mètres;
- elle doit mesurer cinq mètres de long;
- elle doit épouser la pente naturelle du terrain.
Cette cuve est schématisée ci-contre.
![$$(-1.8,-0.5)(7,5)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\pspolygon(2,0)(2,1.8)(-1.3,2.5)(-1.3,0.7)
\rput(-3.3,0.7){\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}}
\psline(2.1,2.7)(5.4,2)
\psline(-1.3,2.5)(2.1,2.7)
\psline(2,1.8)(5.4,2)
\psline[linewidth=0.5pt](2,1.8)(2,3)\psline[linewidth=0.5pt](-1.3,2.5)(-1.3,3.7)
\psset{arrowsize=2pt 3}
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(2,3)(-1.3,3.7)
\psline[linewidth=0.5pt](2,1.8)(1.2,1.75)\psline[linewidth=0.5pt](2,0)(1.2,-0.05)
\psline[linewidth=0.5pt,arrowsize=8pt]{<->}(1.2,1.75)(1.2,-0.05)
\uput[l](1.2,0.85){2 m}\uput[u](1.35,3.35){5 m}
$$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/1.png)
La partie incurvée est modélisée par la courbe
La courbe
On considère les points
(-0.2,-0.25)(6,2.5)
\psaxes[linewidth=1.25pt](0,0)(0,0)(6,2.5)
\uput[u](2.8,0.2){$\mathcal{C}_f$}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\pscustom[fillstyle=solid,fillcolor=lightgray]
{\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psline(5.437,2)(6,2)
\psline(6,0)(2,0)}
\psframe[fillstyle=solid,fillcolor=lightgray](2,2)
\psdots(2,2)(5.437,2)
\psplot[plotpoints=4000]{2}{5.437}{x 2 div ln x mul x sub 2 add}
\psplot[plotpoints=4000]{3}{5.8}{x 2 add 5.437 sub}
\uput[u](2,2){$A$}
\uput[u](5.437,2){$B$}
\uput[ul](5.75,2.2){$\mathcal{T}$}
\uput[dl](2,0){$I$}
\uput[dr](3.437,0){$D$}
\rput(1,1){Terrain}
\rput(3.2,1.2){Cuve}
\rput(4.7,0.5){Terrain}
\psline[linestyle=dotted,linewidth=1.5pt](2,2)(5.437,2)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/10.png)
Partie A L'objectif de cette partie est d'évaluer le volume de la cuve.
- Justifier que les points
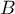 et
et 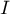 appartiennent à la courbe
appartiennent à la courbe
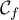 et que l'axe des abscisses est tangent à la courbe
et que l'axe des abscisses est tangent à la courbe
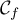 au point
au point 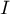 .
.
- On note
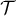 la tangente à la courbe
la tangente à la courbe 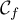 au
point
au
point 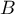 , et
, et 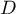 le point d'intersection de la droite
le point d'intersection de la droite 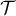 avec l'axe des abscisses.
avec l'axe des abscisses.
- Déterminer une équation de la droite
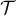 et en
déduire les coordonnées de
et en
déduire les coordonnées de 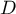 .
.
- On appelle
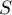 l'aire du domaine délimité par la courbe
l'aire du domaine délimité par la courbe
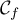 , les droites d'équations
, les droites d'équations 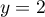 ,
,  et
et  .
.
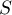 peut être encadrée par l'aire du triangle
peut être encadrée par l'aire du triangle 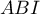 et celle du
trapèze
et celle du
trapèze 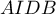 .
.
Quel encadrement du volume de la cuve peut-on en déduire ?
- Déterminer une équation de la droite
-
- Montrer que, sur l'intervalle
![$[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/31.png) ,
la fonction
,
la fonction 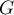 définie par
définie par
![\[G(x)=\dfrac{x^2}{2}\ln \lp\dfrac{x}{2}\rp-\dfrac{x^2}{4}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/33.png)
est une primitive de la fonction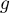 définie par
définie par
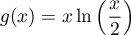 .
.
- En déduire une primitive
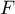 de la fonction
de la fonction 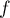 sur
l'intervalle
sur
l'intervalle ![$[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/38.png) .
.
- Déterminer la valeur exacte de l'aire
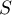 et en déduire une
valeur approchée du volume
et en déduire une
valeur approchée du volume 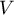 de la cuve au
de la cuve au 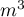 près.
près.
- Montrer que, sur l'intervalle
Partie B Pour tout réel
On admet que, pour tout réel
{\n}}
}
\pspolygon[fillstyle=solid,fillcolor=gray](2,0.1)(2,1.5)(0.35,2.3)(0.35,0.9)
\pspolygon[fillstyle=solid,fillcolor=gray](2,1.5)(0.35,2.3)(3.37,2.47)(5.08,1.7)
\pscustom[fillstyle=solid,fillcolor=gray]{
\pscurve(2,0.1)(3,0.316)(4,0.87)(5.08,1.75)
\psline(5.08,1.75)(2,1.5)
}
\pspolygon(5.437,2.1)(2,1.85)(0.35,2.7)(3.787,2.95)
\psline(2,1.85)(2,1.5)
\psline(0.35,2.7)(0.35,2.3)
\pscurve(0.35,0.9)(1.35,1.16)(2.35,1.72)(3.35,2.5)(3.787,2.95)
\psline[linestyle=dotted,linewidth=1.5pt](5.08,0.2)(5.08,1.75)(0,1.37)
\uput[d](5.2,0.3){$x$}
\uput[l](0,1.37){$f(x)$}
\multido{\n=0+1}{4}{\uput[l](0,\n){\n}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016/50.png)
- Quel volume d'eau, au m
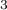 près, y a-t-il dans la cuve lorsque
la hauteur d'eau dans la cuve est de un mètre ?
près, y a-t-il dans la cuve lorsque
la hauteur d'eau dans la cuve est de un mètre ?
- On rappelle que
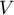 est le volume total de la cuve,
est le volume total de la cuve, 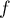 est la
fonction définie en début d'exercice et
est la
fonction définie en début d'exercice et 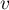 la fonction définie dans
la partie B.
la fonction définie dans
la partie B.
On considère l'algorithme ci-dessous.
Interpréter le résultat que cet algorithme permet d'afficher.
Variables: a est un réel
b est un réelTraitement: a prend la valeur 2
b prend la valeur 2e
Tant que v(b)-v(a)>10-3 faire:
c prend la valeur (a+b)/2Fin Tant que
Si v(c)<V/2, alors:
a prend la valeur cSinonb prend la valeur cFin SiSortie: Afficher f(c)
Correction
Bac S - Amérique du nord, juin 2016 - 6 points
Partie A
Partie B
Cacher la correction
Bac S - Amérique du nord, juin 2016 - 6 points
Partie A
- On a
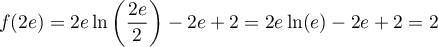 ,
car
,
car 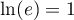 , et donc
, et donc 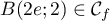 .
.
De même,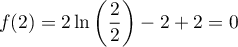 ,
car
,
car 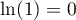 , et donc
, et donc 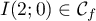 .
.
De plus, en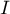 le coefficient directeur de la tangente à
le coefficient directeur de la tangente à
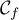 est
est 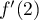 .
.
On a, pour tout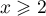 ,
,
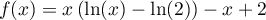 ,
soit
,
soit 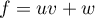 ,
avec
,
avec 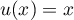 , donc
, donc 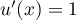 ,
,
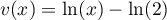 , donc
, donc 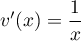 ,
et
,
et 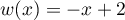 , donc
, donc 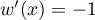 .
.
On a alors,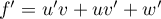 ,
soit
,
soit
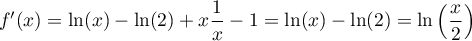 .
.
Ainsi, la tangente à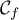 en
en 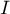 a pour coefficient
directeur
a pour coefficient
directeur 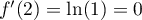 et passe par
et passe par 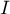 : c'est l'axe des
abscisses.
: c'est l'axe des
abscisses.
-
- Une équation de
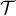 est:
est:
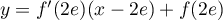 ,
avec
,
avec 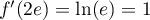 et
et 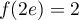 ,
d'où
,
d'où
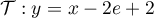 .
.
On a alors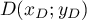 avec
avec 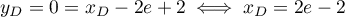 .
Ainsi,
.
Ainsi, 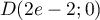 .
.
- L'aire de
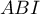 , trangle rectangle en
, trangle rectangle en 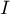 , est
, est
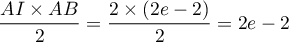
et l'aire du trapèze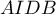 est
est
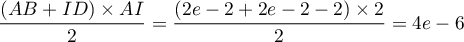 .
.
Ainsi le volume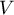 de la cuve est tel que
de la cuve est tel que
![\[5e\leqslant V\leqslant 5(4e-6)\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/39.png)
soit approximativement
![\[17,18\leqslant V\leqslant 24,37\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/40.png)
- Une équation de
-
- On a
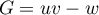 avec
avec 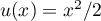 , donc
, donc 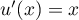 ,
,
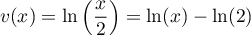 , donc
, donc 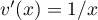 ,
et
,
et 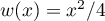 , donc
, donc 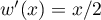 .
.
On a alors,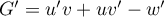 ,
soit
,
soit
![\[\begin{array}{ll}
G'(x)&=x\ln\lp\dfrac{x}2\rp+\dfrac{x^2}{2}\tm\dfrac1x-\dfrac{x}{2}\\[1em]
&=x\ln\lp\dfrac{x}{2}\rp+\dfrac{x}{2}-\dfrac{x}{2}\\[.8em]
&=g(x)\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/49.png)
ce qui montre que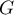 est bien une primitive de
est bien une primitive de 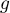 .
.
- On en déduit qu'une primitive de
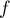 définie par
définie par
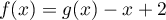 est donnée par
est donnée par
![\[F(x)=G(x)-\dfrac12x^2+2x\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/54.png)
- On peut alors calculer l'intégrale:
![\[\begin{array}{ll}
S&\dsp=\int_2^{2e}\Bigl(2-f(x)\Bigr)dx\\[1em]
&=\Bigl[ 2x-F(x)\Bigr]_2^{2e}\\[1em]
&=\Bigl[ -G(x)+\dfrac12x^2\Bigr]_2^{2e}\\[1em]
&=-G(2e)+\dfrac12(2e)^2-\Bigl(-G(2)+\dfrac122^2\Bigr)\\[.7em]
&=G(2)-G(2e)+2e^2-2
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/55.png)
avec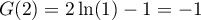 ,
et
,
et 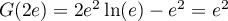 ,
donc
,
donc
![\[S=-1-e^2+2e^2-2=e^2-3\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/58.png)
et on en déduit le volume de la cuve: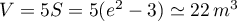 .
.
- On a
Partie B
- Le volume est
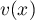 avec
avec 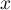 tel que
tel que 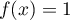 .
On cherche donc à résoudre l'équation
.
On cherche donc à résoudre l'équation 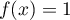 ,
avec
,
avec 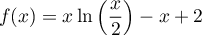 .
.
On ne sait pas résoudre excactement cette équation. On peut par contre le faire de manière approchée, en utilisant le théorème des valeurs intermédiaires.
On sait que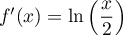 , d'après A.1.
et donc, comme
, d'après A.1.
et donc, comme 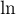 est strictement croissante sur
est strictement croissante sur 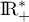 ,
que pour tout
,
que pour tout ![$x\in[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/68.png) ,
,
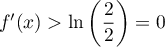 .
.
Ainsi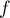 est strictement croissante sur
est strictement croissante sur ![$[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/71.png) , avec de plus
, avec de plus
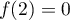 et
et 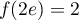 .
On en déduit, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
qu'il existe une unique solution
.
On en déduit, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
qu'il existe une unique solution ![$\alpha\in[2;2e]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/74.png) à l'équation
à l'équation
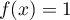 .
.
Avec la calculatrice (à l'aide d'un tableau de valeurs, ou par dichotomie par exemple), on trouve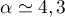 , et alors
le volume est de
, et alors
le volume est de 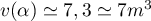 .
.
- Cet algorithme est un algorithme de recherche par dichotomie.
Il permet de chercher les valeurs d'un encadrement![$[a;b]$](/Generateur-Devoirs/TS/ChapLogarithme/ex2-Amerique-nord-juin-2016_c/78.png) pour lequel
la hauteur
pour lequel
la hauteur 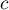 correspond à la moitié de la cuve.
correspond à la moitié de la cuve.
Cet encadrement permet d'avoir un résultat précis à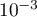 près.
près.
Cacher la correction
Tags:LogarithmePrimitive
Voir aussi:
