Exercice type Bac
Suite, logarithme, limites
Télécharger l'énoncé
L'objectif de ce problème est l'étude de la suite
définie par,
pour tout entier 
non nul,
- Question de cours.
Déterminer la limite:
.
- Etude d'une fonction auxiliaire.
On considère la fonction
définie sur 
par l'expression 
- Déterminer la dérivée
de la fonction 
.
- Déterminer la limite en
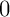et en 
de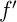 
.
- Démontrer que la dérivée
de la fonction 
s'écrit
.
En déduire alors le sens de variation de la fonction 
.
- Déduire des questions précédentes le signe de
et
le sens de variation de la fonction 
.
- On pose
.
Donner l'expression de 
, puis la limite
.
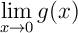En déduire
.
Interpréter graphiquement ce résultat.
- En utilisant les résultats précédents,
tracer l'allure de la courbe
représentative de la
fonction 
.
- Déterminer la dérivée
- Etude de la suite
.
- Exprimer le terme général
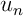, pour 
un
entier naturel non nul, à l'aide de la fonction 
.
- En déduire le sens de variation de la suite
ainsi que
sa limite.
- Exprimer le terme général
Tous les cours de terminale S
Tous les cours et exercices corrigés
Haut de la page
