Construction de la fonction exponentielle -- Méthode d'Euler
Y. Morel
À partir de ces deux seules informations, on peut construire approximativement la fonction et sa courbe, c'est-à-dire qu'on peut calculer approximativement la valeur
Méthode d'Euler: approximation des valeurs de 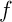
L'information principale sur ![\[f'(x)=\lim_{h\to0}\dfrac{f(x+h)-f(x)}h\]](Construction-exponentielle-methode-Euler-IMG/11.png)
Ainsi, pour un nombre
![\[f'(x)\simeq\dfrac{f(x+h)-f(x)}h\]](Construction-exponentielle-methode-Euler-IMG/13.png)
Plus
Maintenant, comme
![\[f(x)\simeq\dfrac{f(x+h)-f(x)}h\]](Construction-exponentielle-methode-Euler-IMG/16.png)
soit, en isolant
ou encore
En particulier, en partant de
et comme
On a donc
- pour
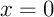 ,
, 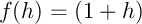
- pour
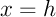 ,
, 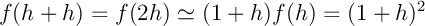 ,
,
- pour
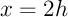 ,
,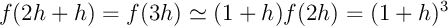 ,
,
- … …
- pour tout entier
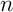 ,
, 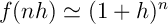
On balaye ainsi, par pas de
Pour calculer une valeur particulière
soit finalement
Calcule de 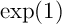
On peut maintenant donner une valeur approchée de
- Pour
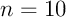 ,
, 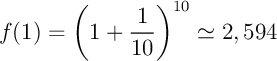
- Pour
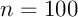 ,
, 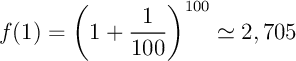
- Pour
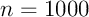 ,
, 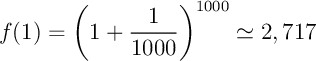
- …
Courbe représentative de l'exponentielle
On peut de même calculer toute valeur souhaitéeOn trace donc la courbe de la "vraie"** fonction exponentielle et celles des fonctions définies par
{$\i$}}
\psplot[linewidth=1.8pt,linecolor=red]{-1}{8}{2.71828 x exp}
\psplot[linewidth=1.8pt,linecolor=blue]{-1}{6}{1 x 10 div add 10 exp}
\psplot[linewidth=1.8pt,linecolor=cyan]{-1}{6}{1 x 50 div add 50 exp}
\psplot[linewidth=1.8pt,linecolor=magenta]{-1}{7.6}{1 x 5 div add 5 exp}
%\pspolgon(
\psline[linewidth=2.5pt,linecolor=red](.5,45)(1,45)\rput[l](1.2,44){$\exp$}
\psline[linewidth=2.5pt,linecolor=cyan](.5,41)(1,41)\rput[l](1.2,41){$n=50$}
\psline[linewidth=2.5pt,linecolor=blue](.5,37)(1,37)\rput[l](1.2,37){$n=10$}
\psline[linewidth=2.5pt,linecolor=magenta](.5,33)(1,33)\rput[l](1.2,33){$n=5$}
\end{pspicture*}\]](Construction-exponentielle-methode-Euler-IMG/57.png)
- *
- Pour utiliser la fonction exponentielle en python (et d'autres comme le logarithme, les fonctions trigonométriques, … ), il faut la charger depuis la bibliothèque des fonctions mathéamtiques:
from math import exp
exp(1) - **
- La fonction exponentielle n'a pas d'expression algébrique "simple" (comme la fonction carré, un polynôme …).
La "vraie courbe" de l'exponentielle est en fait tracée en utilisant des calculs approchés, comme ceux menés ici.
Les méthodes de calcul des valeurs de l'exponentielle par une calculatrice ou un ordinateur sont juste plus efficaces: c'est-à-dire la précision meilleure qu'avec la méthode d'Euler et pour un nombre plus faible de calculs.
Trouver ce genre de méthodes plus efficaces est le champ mathématique qui s'appelle l'analyse numérique.
Voir aussi: