Exercice corrigé bac 2015, Nouvelle Calédonie - Suites, algorithme et nombres complexes
Suites, algorithme et suite de nombres complexes
Exercice corrigé de mathématiques: Exercice corrigé bac 2015, Nouvelle Calédonie - Suites, algorithme et suite géométrique de nombres complexes
Exercice - énoncé:
On note 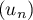 et
et 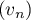 les suites réelles
définies, pour tout entier naturel
les suites réelles
définies, pour tout entier naturel 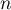 , par
, par
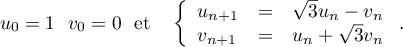
Cacher la correction
- Calculer les valeurs de
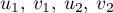 .
.
- On souhaite construire un algorithme qui affiche les valeurs de
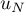 et
et 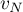 pour un entier naturel
pour un entier naturel 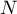 donné.
donné.
- On donne l'algorithme suivant :

Faire fonctionner cet algorithme pour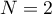 . Pour cela, on
recopiera et complétera le tableau de variables ci-dessous :
. Pour cela, on
recopiera et complétera le tableau de variables ci-dessous :
![\begin{tabular}{|*{3}{c|}}\hline
\hspace*{1cm}$S$\hspace*{1cm} &
\hspace*{1cm}$T$\hspace*{1cm} &
\hspace*{1cm}$K$\hspace*{1cm}\\ \hline
1 &0 &0\\ \hline
$\sqrt{3}$&$\sqrt{3}$&1\rule[-1mm]{0mm}{5mm}\\ \hline
&&\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuitesCplx/ex115.NC/11.png)
- L'algorithme précédent affiche t-il les valeurs de
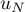 et
et
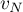 pour un entier
pour un entier 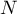 donné ?
donné ?
Dans le cas contraire, écrire sur la copie une version corrigée de l'algorithme proposé qui affiche bien les valeurs de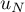 et
et 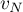 pour un entier
pour un entier 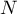 .
.
- On donne l'algorithme suivant :
- On pose, pour tout entier naturel
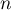 ,
,
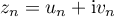 .
.
On note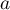 le nombre complexe
le nombre complexe 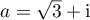 .
.
- Démontrer que, pour tout entier naturel
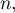
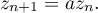
- Écrire
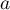 sous forme exponentielle.
sous forme exponentielle.
- En déduire que, pour tout entier naturel
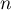 ,
,
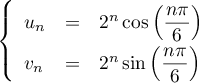
- Démontrer que, pour tout entier naturel
Correction exercice
-
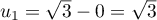 ;
;
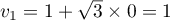 ;
;
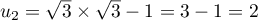 ;
;
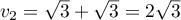 .
.
-
-
![\begin{tabular}{|l|l|c|}\hline
$S$ &$T$ &$K$\\ \hline
1 &0 &0\\ \hline
$\sqrt{3}$ &$\sqrt{3}$ &1\rule[-1mm]{0mm}{5mm}\\ \hline
$3-\sqrt{3}$&$6-\sqrt{3}$ &$2$\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuitesCplx/ex115.NC_c/5.png)
Les valeurs trouvées pour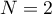 ne correspondent pas à celles de
ne correspondent pas à celles de
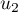 et
et 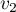 .
.
L'algorithme n'affiche donc pas les valeurs de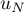 et
et 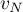 .
.
Une version modifiée de l' algorithme est par exemple :

-
-
-
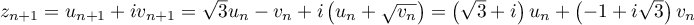 .
.
Or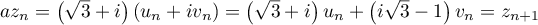 .
.
-
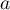 pour module
pour module 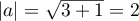 .
D'où
.
D'où 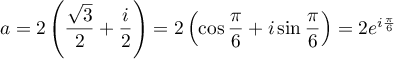 .
.
- La suite
 est une suite géométrique de raison
est une suite géométrique de raison 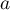 et de premier terme
et de premier terme 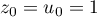 .
.
Par conséquent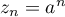 pour tout entier naturel
pour tout entier naturel 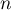 ,
soit
,
soit 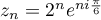 .
.
Enfin en prenant la partie réelle et la partie imaginaire :
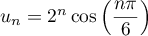 et
et
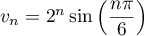 .
.
-
Cacher la correction
Voir aussi: