Exercice corrigé bac 2014 sur les suites, intégrales et la fonction exponentielle
Suite récurrente définie par une fonction, démonstration par récurrence, et limite
Exercice corrigé de mathématiques: Exercice corrigé Bac: exponentielle, suite d'intégrales
Exercice - énoncé:
Bac S, 19 juin 2014, 5 points
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par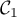 la courbe représentative de la fonction
la courbe représentative de la fonction 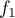 définie sur
définie sur 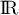 par:
par:
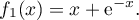
Partie B
L'objet de cette partie est d'étudier la suite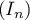 définie sur
définie sur 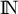 par:
par:
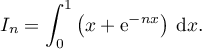
Partie A
Partie B
Cacher la correction
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par
- Justifier que
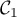 passe par le point A de coordonnées
passe par le point A de coordonnées 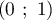 .
.
- Déterminer le tableau de variation de la fonction
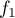 . On
précisera les limites de
. On
précisera les limites de 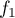 en
en 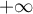 et en
et en 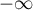 .
.
Partie B
L'objet de cette partie est d'étudier la suite
- Dans le plan muni d'un repère orthonormé
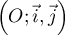 ,
pour tout entier
naturel
,
pour tout entier
naturel 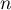 , on note
, on note 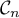 la courbe représentative de la
fonction
la courbe représentative de la
fonction 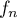 définie sur
définie sur 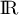 par
par
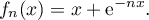
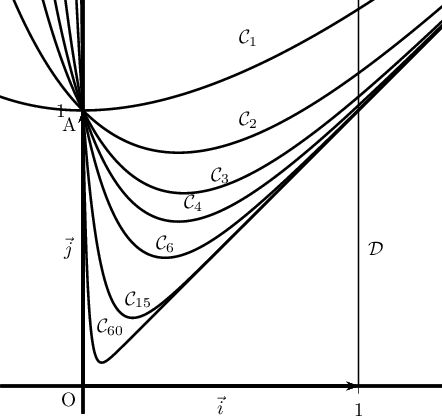
Sur le graphique ci-dessous on a tracé la courbe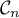 pour plusieurs valeurs de l'entier
pour plusieurs valeurs de l'entier 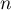 et la droite
et la droite 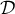 d'équation
d'équation 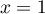 .
.
- Interpréter géométriquement l'intégrale
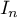 .
.
- En utilisant cette interprétation, formuler une conjecture sur
le sens de variation de la suite
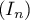 et sa limite
éventuelle. On précisera les éléments sur lesquels on s'appuie
pour conjecturer.
et sa limite
éventuelle. On précisera les éléments sur lesquels on s'appuie
pour conjecturer.
- Interpréter géométriquement l'intégrale
- Démontrer que pour tout entier naturel
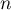 supérieur ou égal à 1,
supérieur ou égal à 1,
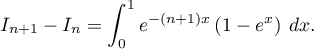
En déduire le signe de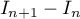 puis démontrer que la suite
puis démontrer que la suite
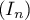 est convergente.
est convergente.
- Déterminer l'expression de
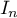 en fonction de
en fonction de 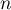 et
déterminer la limite de la suite
et
déterminer la limite de la suite 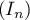 .
.
Correction exercice
Partie A
- On a
 et donc
et donc  .
.
- Comme
 et
et  sont définies et dérivables
sur
sont définies et dérivables
sur  ,
,  est aussi définie et dérivable sur
est aussi définie et dérivable sur  , comme somme
et composéee de fonctions définies et dérivables sur
, comme somme
et composéee de fonctions définies et dérivables sur  ,
avec,
pout tout
,
avec,
pout tout  ,
,  .
.
De plus, ,
car la fonction exponentielle est strictement croissante sur
,
car la fonction exponentielle est strictement croissante sur  ,
et ainsi,
,
et ainsi,  .
.
En ,
,  et
et
 , et donc,
par somme des limites,
, et donc,
par somme des limites,  .
.
En ,
,
 , avec
, avec
 et
et
 (croissance comparée en l'infini de
l'exponentielle et des polynômes).
(croissance comparée en l'infini de
l'exponentielle et des polynômes).
Ainsi, , et alors, par
produit des limites,
, et alors, par
produit des limites,
 .
.

Partie B
-
-
 est l'aire sous la courbe
est l'aire sous la courbe  :
l'aire du domaine compris entre les droites verticales
d'équation
:
l'aire du domaine compris entre les droites verticales
d'équation  et
et  , et entre l'axe des abscisses et la
courbe
, et entre l'axe des abscisses et la
courbe  .
.
- Il semblerait que la courbe
 soit en
dessous de la courbe
soit en
dessous de la courbe  .
On peut donc conjecturer que la suite
.
On peut donc conjecturer que la suite  est décroissante.
est décroissante.
Il semblerait de plus que lorsque devient grand, la courbe
devient grand, la courbe
 se rapproche de la diagonale du carré de côté
se rapproche de la diagonale du carré de côté
 .
On peut ainsi conjecturer que la suite
.
On peut ainsi conjecturer que la suite  est
convergente, de limite
est
convergente, de limite  .
.
-
- Pour tout entier
 ,
,

car .
.
De plus, pour tout ,
,
 ,
et
,
et  , car la fonction exponentielle est strictement
croissante sur
, car la fonction exponentielle est strictement
croissante sur  , et donc,
, et donc,  .
.
On en déduit que pour tout ,
,
 ,
et donc que
,
et donc que

Ainsi, la suite est décroissante.
est décroissante.
Comme pour tout et pour tout entier
et pour tout entier  ,
,
 , et donc,
, et donc,  ,
on a
,
on a  .
.
Ainsi, est une suite décroissante et minorée par 0:
est une suite décroissante et minorée par 0:
 est donc convergente.
est donc convergente.
- Pour tout entier
 ,
,

Comme et
et  ,
on a donc,
,
on a donc,
 ,
ce qui démontre la conjecture émise au début de cette partie.
,
ce qui démontre la conjecture émise au début de cette partie.
Cacher la correction
Voir aussi: