Exercice (type) bac - Statistiques et probabilités
Production de boules sphériques
Exercice corrigé de mathématiques: Exercice corrigé - Statistiques et probabilités, moyenne, écart-type et loi normale
Exercice - énoncé:
Une entreprise produit des boules sphériques en grande quantité.
Le responsable qualité cherche à analyser la production.
Il mesure pour cela le diamètre (en millimètres) des boules d'un
échantillon de 50 pièces, et obtient les résultats suivants:

Une boule est dite conforme si son diamètre appartient à
l'intervalle
appartient à
l'intervalle  .
.
Cacher la correction

Une boule est dite conforme si son diamètre
 appartient à
l'intervalle
appartient à
l'intervalle  .
.
-
- Quel est, dans l'échantillon, le pourcentage de boules non-conformes ?
- Déterminer, pour cet échantillon, la moyenne et l'écart-type du diamètre des boules, arrondis au dixième.
- L'étude statistique permet de modéliser la loi de la variable
aléatoire
 mesurant le diamètre d'une boule par la loi normale de
paramètres
mesurant le diamètre d'une boule par la loi normale de
paramètres  et
et  , la moyenne et l'écart-type trouvés
ci-dessus.
, la moyenne et l'écart-type trouvés
ci-dessus.
- Calculer la probabilité pour qu'une boule prise au hasard soit conforme.
- Quelle valeur devrait prendre l'écart-type pour que, sans changer la moyenne, la probabilité qu'une boule soit non-conforme soit égale à 0,1 ?
Correction exercice
-
- Il y a
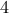 boules non-conformes sur 50, soit un pourcentage de
boules non-conformes sur 50, soit un pourcentage de
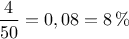 .
.
- La moyenne est: ;
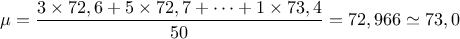 .
.
La variance est alors: soit l'écart-type:
soit l'écart-type: 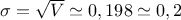 .
.
- Il y a
-
- Soit
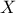 la variable aléatoire égale au diamètre d'une boule
prise au hasard.
Alors
la variable aléatoire égale au diamètre d'une boule
prise au hasard.
Alors 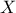 suit la loi
suit la loi 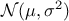 ,
et
,
et 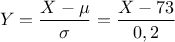 suit la loi normale centrée réduite
suit la loi normale centrée réduite 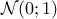 .
.
La probabilité pour qu'une boule prise au hasard soit conforme est alors, en notant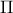 la fonction de répartition de la loi normale centrée
réduite:
la fonction de répartition de la loi normale centrée
réduite:

- On cherche l'écart-type
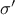 tel que
tel que
 .
.
Soit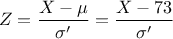 ,
alors
,
alors  suit la loi
suit la loi  et,
et,
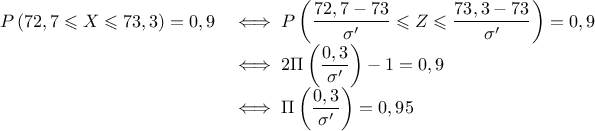
On trouve, à la calculatrice (ou avec la table de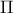 ):
):
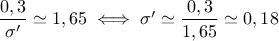 .
.
- Soit
Cacher la correction
Voir aussi: