Exercice bac corrigé - Probabilités: Bac S, juin 2014
Test de dépistage: probabilités conditionnelles, loi normale
Exercice corrigé de mathématiques: Exercice corrigé - Probabilités: Bac S juin 2014, Test de dépistage: probabilités conditionnelles, loi normale
Exercice - énoncé:
Les parties A et B peuvent être traitées indépendamment.
Partie A
Un laboratoire pharmaceutique propose des tests de dépistage de diverses maladies. Son service de communication met en avant les caractéristiques suivantes:
Partie B
La chaine de production du laboratoire fabrique, en très grande quantité, le comprimé d'un médicament.
Partie A
Partie B
Cacher la correction
Partie A
Un laboratoire pharmaceutique propose des tests de dépistage de diverses maladies. Son service de communication met en avant les caractéristiques suivantes:
- la probabilité qu'une personne malade présente un test positif est
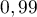 ;
;
- la probabilité qu'une personne saine présente un test positif est
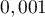 .
.
- Pour une maladie qui vient d'apparaître, le laboratoire élabore
un nouveau test.
Une étude statistique permet d'estimer que le pourcentage de
personnes malades parmi la population d'une métropole est égal à
0,1 %.
On choisit au hasard une personne dans cette population et on lui
fait subir le test.
On note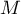 l'événement "la personne choisie est malade"
et
l'événement "la personne choisie est malade"
et 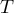 l'événement "le test est positif".
l'événement "le test est positif".
- Traduire l'énoncé sous la forme d'un arbre pondéré.
- Démontrer que la probabilité
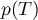 de l'évènement
de l'évènement 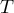 est
égale à
est
égale à 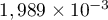 .
.
- L'affirmation suivante est-elle vraie ou fausse ?
Justifier la réponse.
Affirmation: "Si le test est positif, il y a moins d'une chance sur deux que la personne soit malade".
- Le laboratoire décide de commercialiser un test dès lors que la
probabilité qu'une personne testée positivement soit malade est
supérieure ou égale à
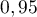 .
On désigne par
.
On désigne par 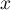 la proportion de personnes atteintes d'une
certaine maladie dans la population.
la proportion de personnes atteintes d'une
certaine maladie dans la population.
A partir de quelle valeur de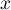 le laboratoire commercialise-t'il
le test correspondant ?
le laboratoire commercialise-t'il
le test correspondant ?
Partie B
La chaine de production du laboratoire fabrique, en très grande quantité, le comprimé d'un médicament.
- Un comprimé est conforme si sa masse est comprise entre 890 et
920 mg.
On admet que la masse en milligrammes d'un comprimé pris au hasard
dans la production peut être modélisée par une variable aléatoire
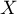 qui suit la loi normale
qui suit la loi normale 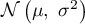 ,
de moyenne
,
de moyenne 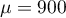 et d'écart-type
et d'écart-type 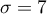 .
.
- Calculer la probabilité qu'un comprimé prélevé au hasard soit
conforme. On arrondira à
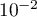 .
.
- Déterminer l'entier positif
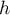 tel que
tel que
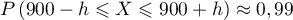 à
à 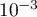 près.
près.
- Calculer la probabilité qu'un comprimé prélevé au hasard soit
conforme. On arrondira à
- La chaine de production a été réglée dans le but d'obtenir au
moins 97 % de comprimés conformes. Afin d'évaluer l'efficacité des
réglages, on effectue un contrôle en prélevant un échantillon de
1000 comprimés dans la production. La taille de la production est
supposée suffisamment grande pour que ce prélèvement puisse être
assimilé à 1000 tirages successifs avec remise.
Le contrôle effectué a permis de dénombrer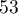 comprimés non
conformes sur l'échantillon prélevé.
comprimés non
conformes sur l'échantillon prélevé.
Ce contrôle remet-il en question les réglages faits par le laboratoire ? On pourra utiliser un intervalle de fluctuation asymptotique au seuil de 95 %.
Correction exercice
Partie A
-
- Le pourcentage de personnes malades est de 0,1%,
ainsi
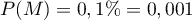 .
.
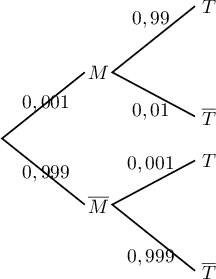
- D'après la loi des probabilités totales
(ou l'utilisation de l'arbre des probabilités),
les événements
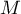 et
et 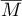 constituant une partition de
l'univers:
constituant une partition de
l'univers:
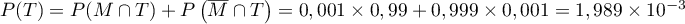 .
.
- L'affirmation fait référence à la probabilité d'être
malade sachant que le test est positif:
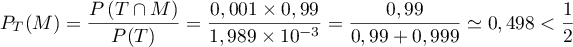 .
.
L'affirmation est donc correcte: si une personne obtient un test positif, alors la probabilité qu'elle soit effectivement malade est (légèrement) inférieure à 0,5, soit un peu moins d'une chance sur deux.
- Le pourcentage de personnes malades est de 0,1%,
ainsi
- On reprend la même démarche, avec maintenant
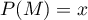 :
:
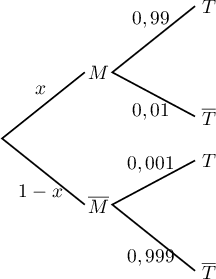
On a alors: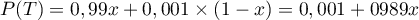 et donc,
et donc,
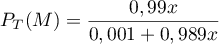 .
.
On cherche alors à résoudre, pour![$x\in[0;1]](/Generateur-Devoirs/TS/ChapProbabilites/ex114_c/11.png) ,
,
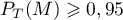 , soit
, soit
![\begin{array}{ll}
\dfrac{0,99x}{0,001 + 0,989x} \geqslant 0,95
&\iff 0,99x \geqslant 0,95 \times (0,001 + 0,989x)
\text{ car } 0,001 + 0,989x \geqslant 0,001>0 \\[0.3cm]
&\iff 0,99x \geqslant 0,00095 + 0,93955x
\iff x \geqslant \dfrac{0,00095}{0,05045} \simeq 0,01883
\enar](/Generateur-Devoirs/TS/ChapProbabilites/ex114_c/13.png)
Le test est donc commercialisable dès lors que la proportion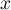 de personnes atteintes par la maladie dans la population
est supérieure à environ
de personnes atteintes par la maladie dans la population
est supérieure à environ 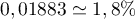 .
.
Partie B
-
- On utilise la calculatrice, qui donne :
 à
à 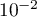 près.
près.
- On pose
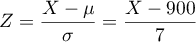 qui est
une variable aléatoire qui suit la loi normale centrée réduite
qui est
une variable aléatoire qui suit la loi normale centrée réduite
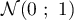 .
.
On a alors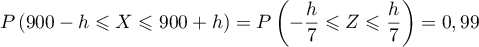 .
.
Or on sait que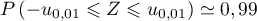 pour
pour 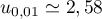 .
.
Ainsi, on doit avoir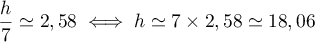 .
.
Puisque le nombre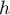 demandé est entier, on arrondit à
demandé est entier, on arrondit à 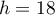 .
.
On peut vérifier à la calculatrice que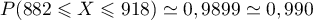 à
à 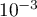 près.
près.
- On utilise la calculatrice, qui donne :
- Puisque la sélection de l'échantillon est assimilée à un tirage
au sort avec remise, on a donc
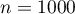 répétitions indépendantes
d'une épreuve de Bernoulli dont le succès est "le comprimé tiré est
conforme" de probabilité
répétitions indépendantes
d'une épreuve de Bernoulli dont le succès est "le comprimé tiré est
conforme" de probabilité 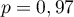 .
.
La variable aléatoire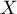 qui est égale au nombre de comprimés non
conformes sur ces 1000 rpétitions suit donc la loi binomiale
qui est égale au nombre de comprimés non
conformes sur ces 1000 rpétitions suit donc la loi binomiale
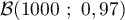 .
.
Le paramètre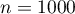 étant suffisamment élevé (
étant suffisamment élevé ( ),
on en déduit que l'intervalle de fluctuation
asymptotique au seuil de
),
on en déduit que l'intervalle de fluctuation
asymptotique au seuil de 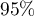 pour la proportion
pour la proportion 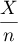 est
est
![\left[ 0,97 - 1,96 \times \dfrac{\sqrt{0,97 \times 0,03}}{\sqrt{1000}}~;
~0,97 + 1,96 \times \dfrac{\sqrt{0,97 \times 0,03}}{\sqrt{1000}}\right]
\simeq \Bigl[ 0,9594~;~0,9806\Bigr]](/Generateur-Devoirs/TS/ChapProbabilites/ex114_c/36.png)
Cela signifie que la proportion de comprimés conformes dans un lot de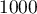 comprimés est comprise dans l'intervalle ci-dessus, avec
une probabilité de 0,95. Comme la proportion de comprimés conformes
constatée dans cet échantillon est de
comprimés est comprise dans l'intervalle ci-dessus, avec
une probabilité de 0,95. Comme la proportion de comprimés conformes
constatée dans cet échantillon est de 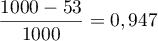 , donc est en dehors de l'intervalle de fluctuation
asymptotique déterminé précédemment, on en déduit que les réglages
faits par le laboratoire ont une forte probabilité d'être à
revoir. La probabilité qu'ils soient corrects bien que l'échantillon
donne une proportion de comprimés conformes en dehors de
l'intervalle de fluctuation n'est que de
, donc est en dehors de l'intervalle de fluctuation
asymptotique déterminé précédemment, on en déduit que les réglages
faits par le laboratoire ont une forte probabilité d'être à
revoir. La probabilité qu'ils soient corrects bien que l'échantillon
donne une proportion de comprimés conformes en dehors de
l'intervalle de fluctuation n'est que de 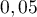 .
.
Cacher la correction
Voir aussi: