Exercice corrigé type bac - Etudes de fonctions avec une exponentielle
Etude d'une fonction avec exponentielle
Exercice corrigé de mathématiques: Exercice corrigé type Bac: Etudes de fonctions avec une exponentielle, utilisation de la dérivée seconde
Exercice - énoncé:
Soit 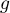 la fonction définie sur
la fonction définie sur 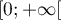 par
par
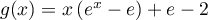 .
.
Soit la fonction définie sur
la fonction définie sur  par
par
 .
.
Cacher la correction
- Soit
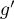 la fonction dérivée de la fonction
la fonction dérivée de la fonction 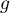 .
Calculer
.
Calculer 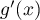 pour tout réel
pour tout réel 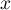 de
de 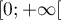 .
.
Vérifier que la fonction dérivée seconde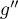 est définie sur
est définie sur
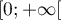 par
par 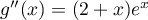 .
.
- En déduire les variations de la fonction
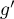 sur
sur
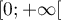 .
.
- Etablir que l'équation
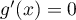 admet une unique solution
admet une unique solution
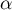 dans l'intervalle
dans l'intervalle 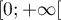 .
.
Déterminer une valeur approchée de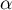 à
à 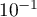 près.
près.
- En déduire les variations de
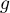 sur
sur 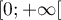 .
.
Correction exercice
Soit
- Pour tout réel
 ,
,
 .
.
Pour tout réel ,
,  .
.
- Pour tout réel
 ,
,  et
et  ,
et donc,
,
et donc,

- La fonction
 est dérivable, donc continue, et strictement
croissante sur
est dérivable, donc continue, et strictement
croissante sur  .
.
De plus, ,
et
,
et  .
.
Ainsi, d'après le théorème des valeurs intermédiaires, l'équation admet une unique solution
admet une unique solution
 dans l'intervalle
dans l'intervalle  .
.
A la calculatrice, on trouve et
et  .
.
Ainsi, , c'est-à-dire
, c'est-à-dire  .
.
- D'après ce qui précède, on a:

Cacher la correction
Voir aussi: