Exercice corrigé type bac - Nombres et plan complexes
Ensemble des points fixes d'une fonction
Exercice corrigé de mathématiques: Exercice corrigé type Bac: Nombres complexes, une fonction dans le plan complexe
Exercice - énoncé:
Le plan est rapporté au repère orthonormal 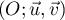 .
.
A tout point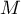 d'affixe
d'affixe 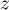 du plan, on associe le point
du plan, on associe le point 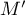 d'affixe
d'affixe 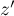 tel que
tel que
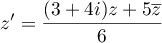 .
.
On définit la fonction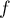 par
par 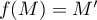 .
.
On définit la fonction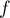 par
par 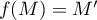 , avec
, avec
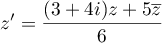 .
.
Cacher la correction
A tout point
On définit la fonction
- On considère les points
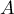 ,
,  et
et  d'affixes respectives
d'affixes respectives
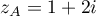 ,
, 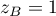 et
et 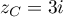 .
.
Déterminer les affixes des points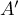 ,
, 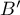 et
et  images
respectives de
images
respectives de 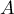 ,
, 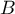 et
et 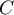 par
par 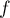 .
Placer les points
.
Placer les points 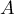 ,
, 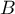 ,
, 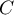 ,
, 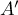 ,
, 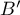 et
et 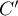 .
.
- On pose
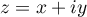 , avec
, avec 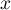 et
et 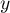 réels.
Déterminer la partie réelle et la partie imaginaire de
réels.
Déterminer la partie réelle et la partie imaginaire de 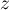 en
fonction de
en
fonction de 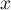 et
et 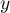 .
.
- Montrer que l'ensemble des points
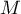 invariants par
invariants par 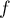 est la
droite
est la
droite 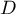 d'équation
d'équation 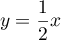 .
.
Tracer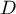 . Que remarque-t-on ?
. Que remarque-t-on ?
(Indication: un point invariant par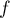 , ou point fixe,
est un point
, ou point fixe,
est un point 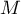 tel que
tel que 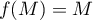 ).
).
- Soit
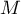 un point quelconque du plan et
un point quelconque du plan et 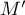 son image par
son image par 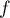 .
.
Montrer que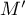 appartient à la droite
appartient à la droite 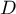 .
.
Correction exercice
On définit la fonction
- On considère les points
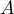 ,
, 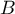 et
et 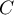 d'affixes respectives
d'affixes respectives
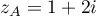 ,
, 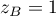 et
et 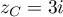 .
.
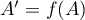 , avec
, avec
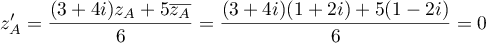 .
.
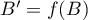 , avec
, avec
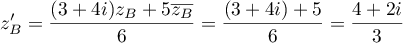
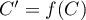 , avec
, avec
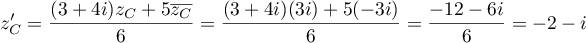
![\psset{unit=1cm,arrowsize=7pt}
\begin{pspicture}(-4,-1.5)(4,3.5)
\psline[linewidth=1.pt]{->}(-3.4,0)(4.2,0)
\psline[linewidth=1.pt]{->}(0,-1.2)(0,3.6)
\psline[linewidth=1.8pt]{->}(0,0)(0,1)\rput(-0.3,0.5){$\vec{v}$}
\psline[linewidth=1.8pt]{->}(0,0)(1,0)\rput(0.5,-0.25){$\vec{u}$}
\rput(1,2){$\tm$}\rput(1.3,2){$A$}
\rput(1,0){$\tm$}\rput(1.2,-0.3){$B$}
\rput(0,3){$\tm$}\rput(-0.3,3){$C$}
\rput(0,0){$\tm$}\rput(-.3,-0.3){$A'$}
\rput(1.3333,0.66666){$\tm$}\rput(1.6,0.5){$B'$}
\rput(-2,-1){$\tm$}\rput(-2.3,-0.8){$C'$}
% D
\psplot{-2.8}{4.2}{0.5 x mul}\rput(3.5,2){$D$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapComplexes/ex7_c/16.png)
-
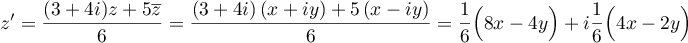
Ainsi, la partie réelle de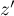 est
est
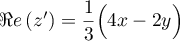 ,
et sa partie imaginaire
,
et sa partie imaginaire
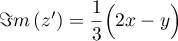 .
.
- Soit un point
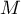 d'affixe
d'affixe 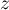 tel que
tel que 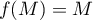 ,
alors on a
,
alors on a 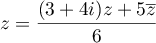 ,
,
et, d'après le calcul précédent, si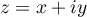 , alors
, alors
![$\la\begin{array}{ll}
x=\dfrac13\Bigl( 4x-2y\Bigr)\\[0.4cm]
y=\dfrac13\Bigl( 2x-y\Bigr)\enar\right.
\iff
\la\begin{array}{ll}
x-2y=0\\[0.4cm]
-2x+4y=0
\enar\right.](/Generateur-Devoirs/TS/ChapComplexes/ex7_c/26.png) .
.
Ces deux équations sont équivalentes, et l'ensemble des points invariants est la droite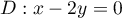 .
On remarque que les points
.
On remarque que les points 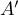 ,
, 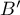 et
et 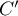 sont des points de
sont des points de
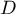 .
.
- Soit
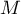 d'affixe
d'affixe 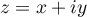 ,
, 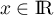 ,
, 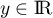 .
Alors
.
Alors 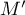 a pour affixe
a pour affixe 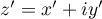 tel que
tel que
![$\la\begin{array}{ll}
x'=\dfrac13\Bigl( 4x-2y\Bigr)\\[0.4cm]
y'=\dfrac13\Bigl( 2x-y\Bigr)\enar\right.](/Generateur-Devoirs/TS/ChapComplexes/ex7_c/38.png) et on vérifie donc bien que
et on vérifie donc bien que 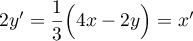 ,
et donc que
,
et donc que 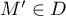 .
.
Ainsi tous les points du plan ont une image par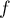 sur la droite
sur la droite
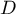 .
.
Cacher la correction
Voir aussi: