Exercice corrigé type bac - ROC sur les nombres complexes

Restitution Organisée des Connaissances: Nombres complexes



Exercice corrigé de mathématiques: Exercice corrigé type Bac, ROC sur les nombres complexes: module et argument d'un nombre complexe

Exercice - énoncé:

ROC
  1. Prérequis: pour tous nombres complexes et ,


    Démontrer par récurrence que, pour tout nombre complexe et pour tout entier naturel ,


    1. Déterminer le module et un argument de .
    2. En déduire une forme trigonométrique de .

Correction exercice


ROC
 
  1. Démontrons par récurrence que, pour tout nombre complexe 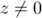et pour tout entier naturel , .
     
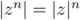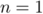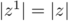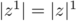    Initialisation: Pour , , et , et donc on a bien , et la propriété est vraie au rang .
     
    Hérédité: Supposons que pour un certain entier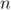 on ait .
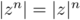    Alors, au rang :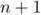
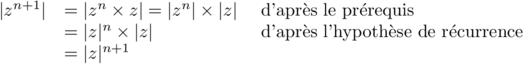
    Ainsi, la propriété est encore vraie au rang .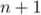
     
    Conclusion: D'après le principe de récurrence, la propriété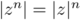 est donc vraie pour tout entier .
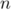    Démontrons par récurrence que, pour tout nombre complexe 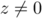et pour tout entier naturel , .
     
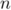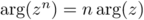    Initialisation: Pour , , 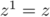et donc on a bien 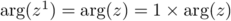, et la propriété est vraie au rang .
     
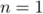    Hérédité: Supposons que pour un certain entier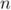 on ait .
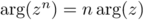    Alors, au rang :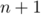
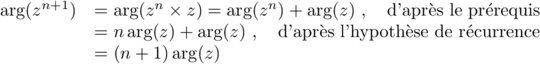
    Ainsi, la propriété est encore vraie au rang .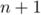
     
    Conclusion: D'après le principe de récurrence, la propriété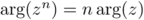 est donc vraie pour tout entier .
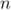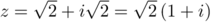    1. , et donc, .
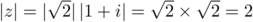      Soit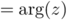 , alors 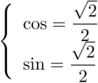, d'où .
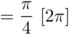    2. On a alors, 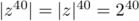, et ,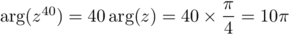
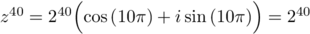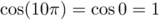      d'où , car , et .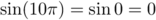


Cacher la correction


Voir aussi:
ccc