Exercice corrigé bac S septembre 2007- Nombres complexes

Nombres complexes et géométrie dans le plan complexe



Exercice corrigé de mathématiques: Exercice corrigé Bac S, septembre 2007: Nombres complexes, géométrie dans le plan complexe

Exercice - énoncé:

(Baccalauréat France métropolitaine, Septembre 2007, 5 points) Soit les nombres complexes :

  1. Écrire sous forme algébrique.
  2. Donner les modules et arguments de , et .
  3. En déduire et .
  4. Le plan est muni d'un repère orthonormal ; on prendra 2 cm comme unité graphique.
    On désigne par , et les points d'affixes respectives , et . Placer le point , puis placer les points et en utilisant la règle et le compas (on laissera les traits de construction apparents).
  5. Écrire sous forme algébrique le nombre complexe .

Correction exercice


  1. On a .
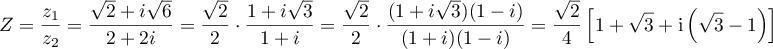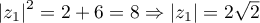    • . On a donc 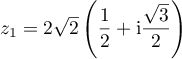. Donc arg.
    • On a de même 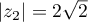, puis 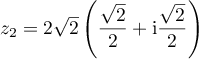. Donc arg.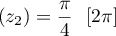
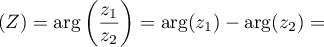
    • Il suit arg 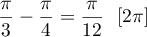. et .
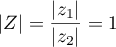  3. On en déduit que 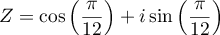et par identification avec la forme algébrique du 1):


  4. On place facilement le point .
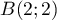    Le point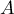 d'affixe 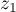est obtenu en construisant la médiatrice du segment .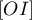
    Le point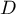 est obtenu en construisant la bissectrice de .
    Le point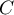 avec la bissectrice de et le cercle de centre et de rayon 1.

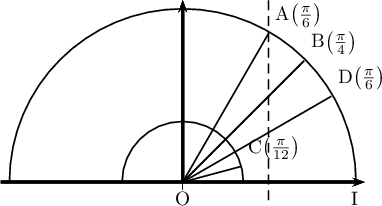
  5. Le module : .
    L'argument : .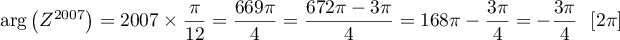
    On a donc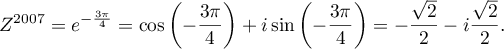


Cacher la correction


Voir aussi:
ccc