Exercice corrigé bac S Centres Etrangers 2010- Nombres complexes
Une application dans le plan complexe: Nombres complexes et géométrie
Exercice corrigé de mathématiques: Exercice corrigé Bac S, Centres Etrangers 2010: Nombres complexes, géométrie dans le plan complexe
Exercice - énoncé:
(Centres étrangers, Juin 2010, 5 points)
Dans le plan complexe  muni d'un repère orthonormal
direct
muni d'un repère orthonormal
direct  d'unité graphique 4 cm, on considère le point A d'affixe
d'unité graphique 4 cm, on considère le point A d'affixe
 et l'application
et l'application  , du plan
, du plan  dans lui·même,
qui au point
dans lui·même,
qui au point  d'affixe
d'affixe  , distinct de A, associe le point
, distinct de A, associe le point  d'affixe
d'affixe  tel que :
tel que :

Cacher la correction
- Déterminer l'affixe des points
 tels que
tels que  .
.
- Démontrer que pour tout point
 distinct de A et de O, on a :
distinct de A et de O, on a :

-
- Soit B le point d'affixe
 .
Placer dans le repère le point B et la médiatrice (
.
Placer dans le repère le point B et la médiatrice ( ) du
segment [OA].
) du
segment [OA].
- Calculer sous forme algébrique l'affixe
 du point B
du point B image du point B par
image du point B par  .
Établir que B
.
Établir que B appartient au cercle
appartient au cercle  de centre O
et de rayon 1.
de centre O
et de rayon 1.
Placer le point B et tracer le cercle
et tracer le cercle  dans le
repère.
dans le
repère.
- En utilisant la question 2, démontrer que, si un point
 appartient à la médiatrice (
appartient à la médiatrice ( ), son image
), son image  par
par  appartient au cercle
appartient au cercle  .
.
- Soit C le point tel que le triangle AOC soit équilatéral
direct.
En s'aidant des résultats de la question 2, construire, à la règle
et au compas, l'image du point C par
 (On laissera apparents
les traits de construction.)
(On laissera apparents
les traits de construction.)
- Soit B le point d'affixe
- Dans cette question, on se propose de déterminer
l'ensemble (
 ) des points
) des points  distincts
de A et de O dont l'image
distincts
de A et de O dont l'image  par
par  appartient à l'axe des
abscisses.
À l'aide de la question 2, retrouver géométriquement la nature de l'ensemble (
appartient à l'axe des
abscisses.
À l'aide de la question 2, retrouver géométriquement la nature de l'ensemble ( ).
).
Correction exercice
- On a
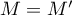 lorsque
lorsque  , soit:
, soit:

soit donc, :
les points d'affixes
:
les points d'affixes 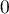 et
et  vérifient
vérifient  .
.
- Pour tout point
 distinct de A et de O, on a:
distinct de A et de O, on a:

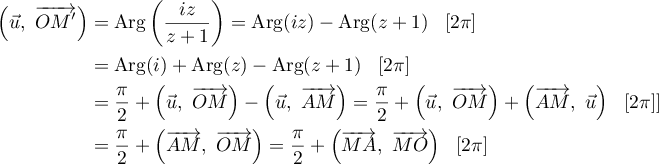
-
- Soit
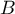 le point d'affixe
le point d'affixe  .
(Voir figure en fin d'exercice)
.
(Voir figure en fin d'exercice)
- Calcul de l'affixe
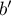 du point
du point  image du point
image du point 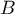 par
par 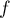 :
:

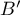 appartient au cercle
appartient au cercle 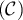 de centre
de centre  et de rayon 1, car:
et de rayon 1, car:

- Si
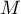 est sur la médiatrice
est sur la médiatrice  , on a
, on a 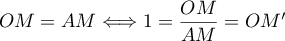 . Ainsi
. Ainsi  est sur le cercle
est sur le cercle  de centre
de centre 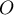 et de rayon 1.
et de rayon 1.
- Soit
 le point tel que le triangle
le point tel que le triangle  soit équilatéral direct.
Le point
soit équilatéral direct.
Le point  est sur le cercle
est sur le cercle  .
On a
.
On a
 .
.
On a de plus, d'après la question 2., ,
et, comme
,
et, comme
 ,
on en déduit que
,
on en déduit que  a comme ordonnée
a comme ordonnée  et se trouve
donc aussi sur la médiatrice de
et se trouve
donc aussi sur la médiatrice de  , avec
, avec 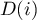 .
.
- Soit
-
Géométriquement, est sur l'axe des abscisses si et
seulement si
est sur l'axe des abscisses si et
seulement si
 .
Soit, d'après la question 2.,
.
Soit, d'après la question 2.,

On en déduit donc que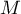 est sur le cercle de diamètre
est sur le cercle de diamètre
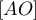 .
.
Cacher la correction
Voir aussi: