Exercice corrigé bac STI2D / STL - Métropole juin 2014 - suite géométrique et algorithmique
Suite géométrique et algorithme
Exercice corrigé de mathématiques: Exercice corrigé du bac STI2D / STL - Métropole juin 2014 - suite géométrique et algorithmique
Exercice - énoncé:
Au cours de son évolution, une tornade se déplace dans un
corridor de quelques centaines de mètres de large sur quelques
kilomètres de long.
Document 1:
L'échelle de Fujita est une échelle servant à classer les tornades par ordre de gravité, en fonction des dégâts qu'elles occasionnent. Une partie de cette échelle est présentée dans le tableau ci-dessous.
![\[\begin{tabular}{|c|c|p{8cm}|}\hline
\rule[-.6cm]{0cm}{1.4cm}
\textbf{Cat\'egorie} &
\begin{minipage}{4.2cm}\textbf{Vitesse des vents en $\text{km}.\text{h}^{-1}$}\end{minipage}
& \multicolumn{1}{c|}{\textbf{D\'eg\^ats occasionn\'es}} \\\hline\hline
F0 & 60 \`a 120 &
\textbf{D\'eg\^ats l\'egers :}
d\'eg\^ats sur chemin\'ees, arbres, fen\^etres,\ldots
\\ \hline
F1 & 120 \`a 180 &
\textbf{D\'eg\^ats mod\'er\'es :}
automobiles renvers\'ees, arbres d\'eracin\'es,\ldots
\\ \hline
F2 & 180 \`a 250 &
\textbf{D\'eg\^ats importants :}
toits arrach\'es, hangars et d\'ependances d\'emolis, \ldots \\ \hline
F3 & 250 \`a 330 &
\textbf{D\'eg\^ats consid\'erables :}
murs ext\'erieurs et toits projet\'es, maisons et b\^atiments de m\'etal
effondr\'es, for\^ets abattues, \ldots
\\ \hline
F4 & 330 \`a 420 &
\textbf{D\'eg\^ats d\'evastateurs :}
murs effondr\'es, objets en acier ou en b\'eton projet\'es comme des
missiles, \ldots
\\ \hline
F5 & 420 \`a 510 &
\textbf{D\'eg\^ats incroyables :}
maisons ras\'ees ou projet\'ees sur de grandes distances, murs ext\'erieurs
et toits arrach\'es sur de gros b\^atiments, \ldots
\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TSTI/Suites/ex2014-Metropole/1.png)
Document 2:
Lors de la formation d'une tornade, on a mesuré la vitesse des vents par un radar météorologique et on a trouvé une vitesse initiale de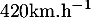 .
.
L'objectif de ce problème est d'estimer la durée de vie de cette tornade.
Dans cet exercice, les résultats seront arrondis à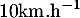 .
.
Cacher la correction
Document 1:
L'échelle de Fujita est une échelle servant à classer les tornades par ordre de gravité, en fonction des dégâts qu'elles occasionnent. Une partie de cette échelle est présentée dans le tableau ci-dessous.
![\[\begin{tabular}{|c|c|p{8cm}|}\hline
\rule[-.6cm]{0cm}{1.4cm}
\textbf{Cat\'egorie} &
\begin{minipage}{4.2cm}\textbf{Vitesse des vents en $\text{km}.\text{h}^{-1}$}\end{minipage}
& \multicolumn{1}{c|}{\textbf{D\'eg\^ats occasionn\'es}} \\\hline\hline
F0 & 60 \`a 120 &
\textbf{D\'eg\^ats l\'egers :}
d\'eg\^ats sur chemin\'ees, arbres, fen\^etres,\ldots
\\ \hline
F1 & 120 \`a 180 &
\textbf{D\'eg\^ats mod\'er\'es :}
automobiles renvers\'ees, arbres d\'eracin\'es,\ldots
\\ \hline
F2 & 180 \`a 250 &
\textbf{D\'eg\^ats importants :}
toits arrach\'es, hangars et d\'ependances d\'emolis, \ldots \\ \hline
F3 & 250 \`a 330 &
\textbf{D\'eg\^ats consid\'erables :}
murs ext\'erieurs et toits projet\'es, maisons et b\^atiments de m\'etal
effondr\'es, for\^ets abattues, \ldots
\\ \hline
F4 & 330 \`a 420 &
\textbf{D\'eg\^ats d\'evastateurs :}
murs effondr\'es, objets en acier ou en b\'eton projet\'es comme des
missiles, \ldots
\\ \hline
F5 & 420 \`a 510 &
\textbf{D\'eg\^ats incroyables :}
maisons ras\'ees ou projet\'ees sur de grandes distances, murs ext\'erieurs
et toits arrach\'es sur de gros b\^atiments, \ldots
\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TSTI/Suites/ex2014-Metropole/1.png)
Document 2:
|
À partir des mesures relevées lors d'observations de phénomènes
semblables, des météorologues ont admis la règle suivante : « la
vitesse des vents dans les tornades diminue régulièrement de 10 %
toutes les 5 minutes » .
On appelle « durée de vie » d'une tornade le temps nécessaire, depuis sa formation, pour que la vitesse des vents devienne inférieure à 120 |
Lors de la formation d'une tornade, on a mesuré la vitesse des vents par un radar météorologique et on a trouvé une vitesse initiale de
L'objectif de ce problème est d'estimer la durée de vie de cette tornade.
Dans cet exercice, les résultats seront arrondis à
-
- Cinq minutes après la mesure initiale, la vitesse des vents
est de
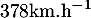 .
.
Vérifier que ce résultat correspond à la règle admise.
À quelle catégorie appartient la tornade à ce moment là ? - Vérifier que, quinze minutes après la mesure initiale, cette tornade occasionne des dégâts classés comme « dégâts considérables» .
- Cinq minutes après la mesure initiale, la vitesse des vents
est de
- Pour déterminer la durée de vie de cette tornade, un étudiant
propose de modéliser le phénomène par une suite géométrique de
raison
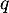 . Il commence à élaborer l'algorithme ci-dessous.
. Il commence à élaborer l'algorithme ci-dessous.
Variables
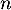 : un nombre entier naturel
: un nombre entier naturel
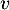 : un nombre réel
: un nombre réel
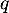 : un nombre réel
: un nombre réel
Initialisation
Affecter à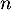 la valeur 0
la valeur 0
Affecter à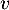 la valeur 420
la valeur 420
Affecter à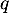 la valeur 0,9
la valeur 0,9
Traitement
Tant que …
…
…
Fin Tant que
Sortie
Afficher
- Justifier la valeur 0,9 dans la phrase « Affecter à
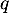 la
valeur 0,9 » .
la
valeur 0,9 » .
- Donner le premier terme et la raison de la suite géométrique proposée par l'étudiant.
- Dans l'algorithme ci-dessus, des pointillés indiquent des parties manquantes.
Recopier la partie relative au traitement et la compléter pour que l'étudiant puisse déterminer la durée de vie de cette tornade. - Expliquer l'instruction « Afficher
 » proposée
par l'étudiant.
» proposée
par l'étudiant.
- Justifier la valeur 0,9 dans la phrase « Affecter à
- On désigne par
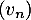 la suite géométrique proposée
par l'étudiant.
la suite géométrique proposée
par l'étudiant.
Exprimer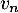 en fonction de
en fonction de 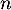 .
.
- Déterminer la durée de vie de cette tornade au sens défini dans le document 2.
Correction exercice
-
- D'après la règle, on devrait avoir une diminution de
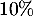 de la vitesse, soit une vitesse de
de la vitesse, soit une vitesse de
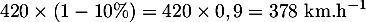 .
Le résultat correspond donc bien à la règle.
.
Le résultat correspond donc bien à la règle.
À ce moment, la tornade appartient à la catégorie F4.
- Quinze minutes après la mesure initiale,
la vitesse des vents est de
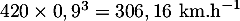 , et la tornade appartient à la
catégorie F3 et occasionne donc des dégâts classés comme «
dégâts considérables» .
, et la tornade appartient à la
catégorie F3 et occasionne donc des dégâts classés comme «
dégâts considérables» .
- D'après la règle, on devrait avoir une diminution de
-
- 0,9 est le coefficient multiplicateur correspondant à une
diminution de
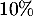 ; c'est la raison de la suite.
; c'est la raison de la suite.
- Le premier terme est
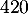 et la raison 0,9.
et la raison 0,9.
-
…
Tant que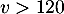
Affecter à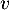 la valeur
la valeur 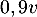
Affecter à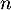 la valeur
la valeur 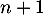
Fin Tant que
…
- La variable
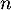 correspond au nombre de diminution de
correspond au nombre de diminution de 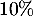 .
Comme les vents diminuent de
.
Comme les vents diminuent de 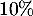 toutes les 5 minutes, le temps
total a affiché est
toutes les 5 minutes, le temps
total a affiché est  .
.
- 0,9 est le coefficient multiplicateur correspondant à une
diminution de
-
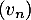 est la suite géométrique de premier terme
est la suite géométrique de premier terme
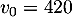 et de raison
et de raison 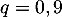 , et ainsi, pour tout entier
, et ainsi, pour tout entier 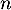 ,
,
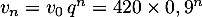 .
.
- On trouve à la calculatrice, ou avec l'algorithme précédent,
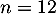 , soit une durée de vie de
, soit une durée de vie de 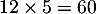 min, soit une heure.
min, soit une heure.
Cacher la correction
Voir aussi: