Bac corrigé STI2D / STL - Métropole juin 2014 - probabilités
Probabilités: loi normale et intervalle de confiance
Exercice corrigé de mathématiques: Exercice corrigé du bac STI2D / STL - Métropole juin 2014 - Probabilités: loi normale et intervalle de confiance
Exercice - énoncé:
Une chocolaterie industrielle fabrique des tablettes de chocolat de
200 grammes. Une machine qui fabrique les tablettes est préréglée afin
de respecter cette masse de 200 grammes.
Lors de la fabrication, toutes les tablettes de chocolat sont pesées et celles dont la masse est inférieure à 195 grammes sont rejetées. L'entreprise ne les commercialisera pas sous cette forme.
Cacher la correction
Lors de la fabrication, toutes les tablettes de chocolat sont pesées et celles dont la masse est inférieure à 195 grammes sont rejetées. L'entreprise ne les commercialisera pas sous cette forme.
- On désigne par
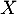 la variable aléatoire qui, à une tablette de
chocolat prélevée au hasard dans la production, associe sa masse en
grammes. On admet que
la variable aléatoire qui, à une tablette de
chocolat prélevée au hasard dans la production, associe sa masse en
grammes. On admet que 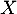 suit la loi normale d'espérance 200 et
d'écart type 2,86.
suit la loi normale d'espérance 200 et
d'écart type 2,86.
Les résultats seront arrondis à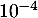 .
.
- Déterminer la probabilité de l'évènement
«
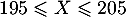 ».
».
- Déterminer la probabilité qu'une tablette de chocolat prise au hasard dans la production ne soit pas rejetée après pesée.
- Déterminer la probabilité de l'évènement
«
- Une étude statistique a établi que, si la machine est bien
réglée, la proportion de tablettes de chocolat rejetées est de
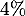 .
.
Afin de vérifier le réglage de la machine, le responsable qualité prélève de manière aléatoire un échantillon de 150 tablettes et observe que 10 tablettes sont rejetées.
Cette observation remet-elle en cause le réglage de la machine ? (On pourra utiliser un intervalle de fluctuation.)
Correction exercice
-
- La probabilité est, à l'aide de la calculatrice,
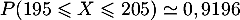 .
.
- La probabilité qu'une tablette de chocolat ne soit pas rejetée
après pesée est, à l'aide de la calculatrice,
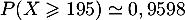 .
.
- La probabilité est, à l'aide de la calculatrice,
- L'intervalle de fluctuation d'une proportion
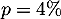 dans un
échantillon de
dans un
échantillon de 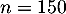 tablettes est
tablettes est
![\[
I=\left[\, p-1,96\sqrt{\dfrac{p(1-p)}{n}}\ ;\
p+1,96\sqrt{\dfrac{p(1-p)}{n}}\,\right]
\simeq \Bigl[\, 0,0086\ ;\ 0,0714\,\Bigr]\]](/Generateur-Devoirs/TSTI/Probabilites/ex2014-Metropole_c/5.png)
Ici, le responsable qualité observe une proportion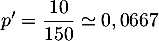 ;
comme
;
comme 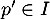 , le réglage de la machine ne peut être remis en
cause.
, le réglage de la machine ne peut être remis en
cause.
Cacher la correction
Voir aussi: