Exercice corrigé bac STI2D / STL - Métropole juin 2014 - QCM: nombres complexes
QCM: nombres complexes
Exercice corrigé de mathématiques: Exercice corrigé du bac STI2D / STL - Métropole juin 2014 - QCM sur les nombres complexes
Exercice - énoncé:
Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses
proposées est exacte. Aucune justification n'est demandée. Une bonne
réponse rapporte un point. Une mauvaise réponse, plusieurs réponses
ou l'absence de réponse à une question ne rapportent ni n'enlèvent
de point.
Indiquer sur la copie le numéro de la question et la réponse correspondante.
On considère les deux nombres complexes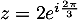 et
et 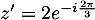 .
.
Indiquer sur la copie le numéro de la question et la réponse correspondante.
On considère les deux nombres complexes
- La forme algébrique de
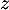 est égale à :
est égale à :

- Le nombre complexe
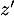 est le nombre complexe :
est le nombre complexe :
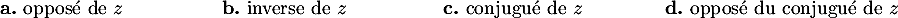
- Le nombre complexe
 :
:
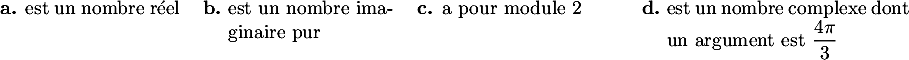
- Un argument du nombre complexe
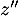 tel que
tel que 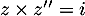 est:
est:

Voir aussi: