Exercice corrigé: Calculs algébriques en géométrie - Repère et coordonnées
Calculs algébriques pour un triangle isocèle ou rectangle
Seconde générale
Exercice corrigé de mathématiques: Exercice corrigé: Valeur d’un réel pour lequel un triangle est isocèle ou rectangle - Calculs algébriques en géométrie - Repère et coordonnées
Exercice - énoncé:
Soit 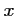 un nombre réel.
On considère les points
un nombre réel.
On considère les points 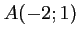 ,
, 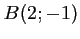 et
et 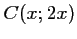 .
.
Soit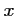 un nombre réel.
On considère les points
un nombre réel.
On considère les points 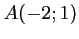 ,
, 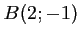 et
et 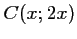 .
.
Cacher la correction
- Montrer que pour tout
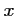 le triangle
le triangle 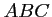 est isocèle de
sommet
est isocèle de
sommet 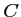 .
.
- Déterminer
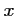 pour que le triangle
pour que le triangle 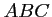 soit rectangle en
soit rectangle en
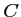 .
.
Correction exercice
Soit
- On calcule les longueurs
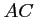 et
et 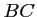 :
:
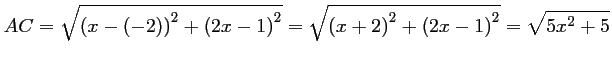
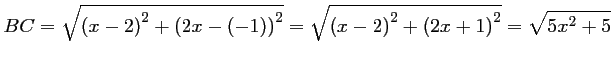
On trouve donc que, pour tout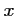 réel,
réel, 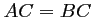 :
le triangle
:
le triangle 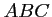 est isocèle de sommet
est isocèle de sommet 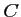 .
.
- On veut que le triangle
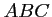 soit rectangle en
soit rectangle en 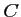 .
Alors, d'après le théorème de Pythagore,
.
Alors, d'après le théorème de Pythagore,
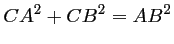
D'après la question précédente, on connaît déjà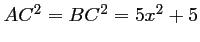 .
.
De plus,
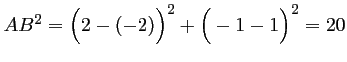 .
.
Pour que le triangle
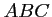 soit rectangle en
soit rectangle en 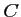 , on doit donc avoir
, on doit donc avoir
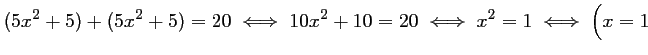 ou
ou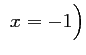
Pour que le triangle soit rectangle en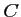 ,
on doit donc avoir
,
on doit donc avoir 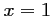 ou
ou 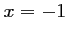 .
.
Cacher la correction
Voir aussi: