Exercice corrigé: Calcul numérique avec des racines carrées et des fractions

Fractions et racines carrées

Seconde générale

Exercice corrigé de mathématiques: Exercice corrigé: calcul numérique avec des racines carrées et des fractions

Exercice - énoncé:

Ecrire sous la forme la plus simple possible (les fractions devront avoir un dénominateur ne contenant pas de racines):
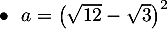
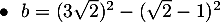
$\bullet\ \ a=\lp\sqrt{12}-\sqrt{3}\rp^2$ $\bullet\ \ b=(3\sqrt{2})^2-(\sqrt{2}-1)^2$
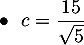
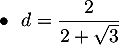
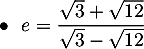
$\bullet\ \ c=\dfrac{15}{\sqrt{5}}$ $\bullet\ \ d=\dfrac{2}{2+\sqrt{3}}$ $\bullet\ \ e=\dfrac{\sqrt{3}+\sqrt{12}}{\sqrt{3}-\sqrt{12}}$

Correction exercice

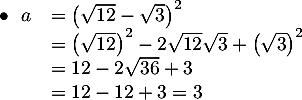
$\begin{array}{ll}\bullet\ \ a&=\lp\sqrt{12}-\sqrt{3}\rp^2\\ &=\lp\sqrt{12}\rp^2-2\sqrt{12}\sqrt{3}+\lp\sqrt{3}\rp^2\\ &=12-2\sqrt{36}+3\\ &=12-12+3=3\enar$

$\begin{array}{ll}\bullet\ \ b&=(3\sqrt{2})^2-(\sqrt{2}-1)^2\\[.4em] &=3^2\sqrt{2}^2-\left( \sqrt{2}^2-2\sqrt{2}+1^2\rp\\[.4em] &=18-\left( 2-2\sqrt{2}+1\rp\\[.6em] &=15+2\sqrt{2}\enar$

$\begin{array}{ll}\bullet\ \ c&=\dfrac{15}{\sqrt{5}}=\dfrac{15\tm\sqrt{5}}{\sqrt{5}\tm\sqrt{5}}\\[.8em] &=\dfrac{15\sqrt{5}}{5}=3\sqrt{5}\enar$

$\begin{array}{ll}\bullet\ \ d&=\dfrac{2}{2+\sqrt{3}}\\[.8em] &=\dfrac{2(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})}\\[1em] &=2(2-\sqrt{3})\enar$

$\begin{array}{ll}\bullet\ \ e&=\dfrac{\sqrt{3}+\sqrt{12}}{\sqrt{3}-\sqrt{12}}\\[1em] &=\dfrac{(\sqrt{3}+\sqrt{12})(\sqrt{3}+\sqrt{12})}{(\sqrt{3}-\sqrt{12})(\sqrt{3}+\sqrt{12})}\\[1em] &=\dfrac{(\sqrt{3})^2+2\sqrt{3}\sqrt{12}+(\sqrt{12})^2}{3-12}\\[1em] &=\dfrac{27}{-9}=-3\enar$

Cacher la correction

Voir aussi: