Exercice corrigé - Produit scalaire - Calcul de distance dans un rectangle
Détermination d'une longueur dans un rectangle
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Produit scalaire - Calcul de distance dans un rectangle: calcul de divers produits scalaires
Exercice - énoncé:
Calcul d'une distance
Cacher la correction
![]() est un rectangle de dimensions
est un rectangle de dimensions ![]() et
et ![]() (
(![]() ).
).
![]() et
et ![]() sont les projetés orthogonaux des points
sont les projetés orthogonaux des points ![]() et
et ![]() sur
la droite
sur
la droite ![]() .
.
|

|
Correction exercice
-
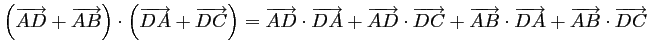 avec,
avec,

-
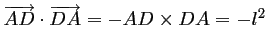 , car les
vecteurs sont colinéaires de sens opposés;
, car les
vecteurs sont colinéaires de sens opposés;

-
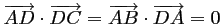 car,
car,
 étant un rectangle,
les vecteurs sont orthogonaux;
étant un rectangle,
les vecteurs sont orthogonaux;

-
 car les vecteurs
sont colinéaires de même sens.
car les vecteurs
sont colinéaires de même sens.
d'où,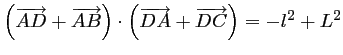 .
.
- Les projetés orthogonaux de
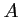 et
et 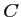 sur la droite
sur la droite 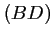 sont
respectivement
sont
respectivement 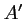 et
et 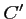 , et donc,
, et donc,
 .
.
- On a
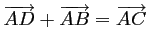 et
et
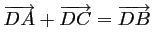 , d'où,
, d'où,
 .
.
On en déduit, d'après les questions précédentes, que:
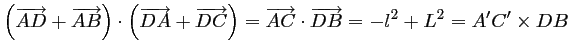
Ainsi,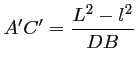
Or, d'après le théorème de Pythagore,
 ,
d'où, au final,
,
d'où, au final,
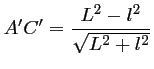 .
.
Cacher la correction
Voir aussi:
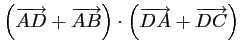 .
.
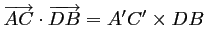 .
.
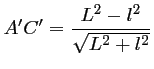 .
.