Exercice corrigé - Probabilités - Loi binomiale
Loi binomiale
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Probabilités - Répétition d'expériences: loi binomiale - Calcul d'espérance
Exercice - énoncé:
Une attraction dans une fête foraine permet de gagner soit un gros
lot, soit une petite peluche.
Cacher la correction
250 cordelettes sont proposées au joueur, dont 30 sont reliées à un gros lot, et les autres à une petite peluche.
Il est bien sûr impossible pour le joueur de déterminer quelle cordelette est reliée à un gros lot ou à une peluche, et les tirages se font donc au hasard.
- Quelle est la probabilité de gagner un gros lot en tirant une
cordelette ?
- Un joueur achète un ticket lui permettant de tirer 3 cordelettes.
On désigne par
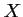 la variable aléatoire égale au nombre de gros lots
gagnés par le joueur.
la variable aléatoire égale au nombre de gros lots
gagnés par le joueur.
- (a) Montrer que
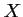 suit une loi binomiale dont on déterminera les
paramètres.
suit une loi binomiale dont on déterminera les
paramètres.
- (b) Déterminer la probabilité de gagner 3 petites peluches.
- (c) Calculer la probabilité de gagner au moins un gros lot.
- (d) Quelle est l'espérance de
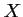 ? Interpréter ce résultat.
? Interpréter ce résultat.
- (a) Montrer que
Correction exercice
- Il y a 250 cordelettes, dont 30 sont reliées à un gros lot.
La probabilité d'en gagner un est donc
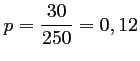 .
.
- (a) Le joueur répète
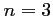 fois l'expérience aléatoire consistant
à tirer au hasard une cordelette, pour la quelle la probabilité de
succès est
fois l'expérience aléatoire consistant
à tirer au hasard une cordelette, pour la quelle la probabilité de
succès est 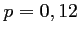 .
.
Ses répétitions sont identiques et indépendantes entre elles.
On en déduit que la variable aléatoire
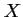 , comptant le nombre de succès
sur ces 3 répétitions, suit la loi binomiale
, comptant le nombre de succès
sur ces 3 répétitions, suit la loi binomiale
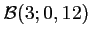 .
.
- (b) L'événement "Gagner 3 petites peluches" est l'événement
"
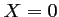 ", dont la probabilité est donc:
", dont la probabilité est donc:
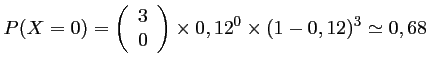
- (c) L'événement "Gagner au moins un gros lot" est l'événement
"
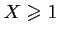 ", dont la probabilité est donc:
", dont la probabilité est donc:
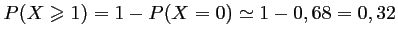
- (d) L'espérance de
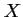 est:
est:
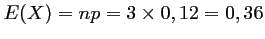 :
En effectuant 3 tirages, le joueur peut espérer obtenir en moyenne
:
En effectuant 3 tirages, le joueur peut espérer obtenir en moyenne
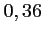 gros lot.
gros lot.
- (a) Le joueur répète
Cacher la correction
Voir aussi: