Exercice corrigé - Polynômes du second et troisième degré - Factorisation, racines et étude du signe
Factorisation, racines et signe
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Factorisation d'un polynômes du troisième degré, recherche de ses racines, et détermination de son signe
Exercice - énoncé:
On considère le polynôme 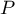 défini par
défini par
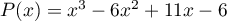 .
.
On considère le polynôme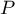 défini par
défini par
 .
.
Cacher la correction
- Vérifier que 1 est une racine de
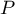 .
.
- Déterminer trois nombres réels
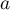 ,
,  et
et 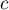 tels que, pour tout réel
tels que, pour tout réel 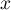 ,
,
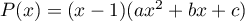 .
.
- Résoudre l'inéquation
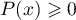 .
.
Correction exercice
On considère le polynôme
-
 et donc 1 est bien une racine de
et donc 1 est bien une racine de  .
.
-
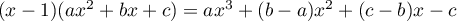 et donc
et donc
 .
.
On trouve donc ,
, 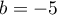 et
et 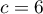 ,
ou encore
,
ou encore
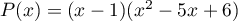 .
.
-
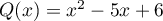 est un trinôme du second degré de
discriminant
est un trinôme du second degré de
discriminant 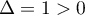 et admet donc deux racines
et admet donc deux racines
 et
et 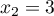 .
On a alors le tableau de signes:
.
On a alors le tableau de signes:
![\[\begin{tabular}{|c|lcccccccr|}\hline
$x$ & $-\infty$ & &1& &2& &3& &$+\infty$
\\\hline
$x-1$& &-& \zb&+& $|$ &+&\zb &$+$&\\\hline
$Q(x)$& &+& $|$ &+& \mbox{$0\hspace{-0.67em}\mid$} &-&\mbox{$0\hspace{-0.67em}\mid$}&+& \\\hline
$P(x)$& &-& \mbox{$0\hspace{-0.67em}\mid$} &+& \mbox{$0\hspace{-0.67em}\mid$} &-&$|$&+& \\\hline
\end{tabular}
\]](/Generateur-Devoirs/1S/Chap1/ex2.0_c/15.png)
On a alors![$P(x)\geqslant0\iff x\in[1;2]\cup[3;+\infty[$](/Generateur-Devoirs/1S/Chap1/ex2.0_c/16.png) .
.
Cacher la correction
Voir aussi: