Exercice corrigé - Etude complète d'une fonction à l'aide d'une fonction auxiliaire
Etude à l'aide d'une fonction auxiliaire
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Etudes de fonctions, à l'aide d'une fonction auxiliaire et du théorème des valeurs intermédiaires
Exercice - énoncé:
- a. Dresser le tableau de variation de
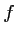 .
.
- b. Tracer la courbe représentative de la fonction
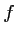 .
.
- a. Dresser le tableau de variation de
- a. Montrer que l'équation
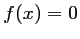 admet une unique solution
admet une unique solution
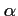 sur
sur
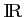 , et que
, et que
![$ \alpha\in[1;2]$](/Generateur-Devoirs/1S/Chap3/ex17_img6.png) .
.
- b. Donner un encadrement à
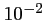 près de
près de 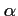 .
.
- c. Déduire de ce qui précède le signe de
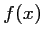 .
.
- a. Montrer que l'équation
- Soit
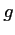 la fonction définie sur
la fonction définie sur
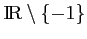 par
l'expression:
par
l'expression:
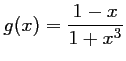 .
.
- a. Déterminer, pour tout nombre
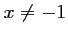 ,
, 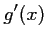 .
.
- b. Dresser alors le tableau de variation de
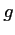 .
.
- a. Déterminer, pour tout nombre
Correction exercice
- a.
Pour tout 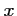 réel,
réel, 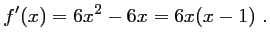
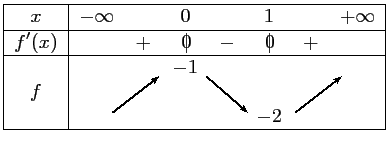
- b.
-
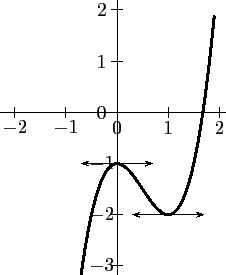
- a.
- On a
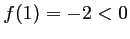 et
et 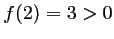 .
De plus,
.
De plus, 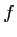 est dérivable, strictement croissante sur
est dérivable, strictement croissante sur ![$ [1;2]$](/Generateur-Devoirs/1S/Chap3/ex17_c_img8.png) ,
donc, d'après le théorème des valeurs intermédiaires,
l'équation
,
donc, d'après le théorème des valeurs intermédiaires,
l'équation 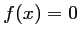 admet sur
admet sur ![$ [1;2]$](/Generateur-Devoirs/1S/Chap3/ex17_c_img8.png) une unique solution
une unique solution
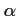 .
.
De plus, sur
![$ ]-\infty;0]$](/Generateur-Devoirs/1S/Chap3/ex17_c_img11.png) ,
, 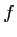 est dérivable et strictement
croissante avec
est dérivable et strictement
croissante avec 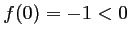 , et donc l'équation
, et donc l'équation 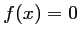 n'admet aucune solution sur
n'admet aucune solution sur
![$ ]-\infty;0]$](/Generateur-Devoirs/1S/Chap3/ex17_c_img11.png) .
.
De même, sur
![$ [0;1]$](/Generateur-Devoirs/1S/Chap3/ex17_c_img13.png) ,
, 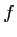 est dérivable et strictement
décroissante avec
est dérivable et strictement
décroissante avec 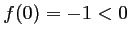 , donc l'équation
, donc l'équation 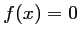 n'admet
aucune solution sur
n'admet
aucune solution sur ![$ [0;1]$](/Generateur-Devoirs/1S/Chap3/ex17_c_img13.png) .
.
Enfin, sur
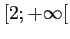 ,
, 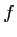 est dérivable et strictement
croissante avec
est dérivable et strictement
croissante avec 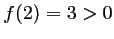 , et donc l'équation
, et donc l'équation 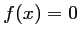 n'admet
aucune solution sur
n'admet
aucune solution sur
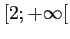 .
.
Finalement, l'équation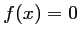 admet une unique solution
admet une unique solution 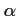 sur
sur
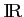 et
et
![$ \alpha\in[1;2]$](/Generateur-Devoirs/1S/Chap3/ex17_c_img16.png) .
.
- b.
- A l'aide de la calculatrice (avec un tableau de valeurs, ou
avec la méthode par dichotomie), on trouve
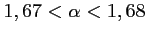 .
.
- c.
- On en déduit le signe de
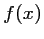 :
:
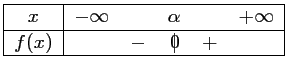
- Soit
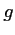 la fonction définie sur
la fonction définie sur
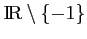 par
l'expression:
par
l'expression:
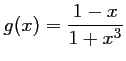 .
.
- a.
- Pour tout nombre
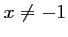 ,
,
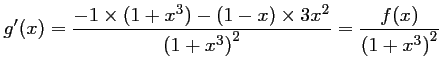
- b.
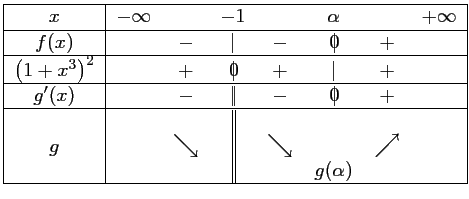
Cacher la correction
Voir aussi: