Exercice corrigé - Etude d'une fonction avec un paramètre
Sens de variation selon le paramètre
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Dérivée et étude d'une fonction avec un paramètre
Exercice - énoncé:
![]() est la fonction définie sur
est la fonction définie sur
![]() par:
par:
![]() .
.
- On suppose
 .
Déterminer les variations de
.
Déterminer les variations de 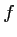 .
.
- On suppose maintenant
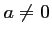 .
.
- a) Pour tout nombre
 , calculer
, calculer 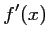 .
.
- b) Pour quelles valeurs de
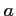 , la fonction
, la fonction 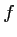 est-elle
croissante sur
est-elle
croissante sur
 ?
?
- a) Pour tout nombre
Correction exercice
- On suppose
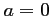 , et on a donc
, et on a donc
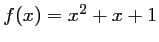 .
Pour tout
.
Pour tout 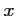 réel,
réel,
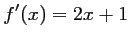 .
Ainsi,
.
Ainsi, 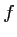 est décroissante sur
est décroissante sur
![$ ]-\infty;-\frac{1}{2}]$](/Generateur-Devoirs/1S/Chap3/ex8_c_img6.png) et croissante sur
et croissante sur
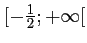 .
.
- On suppose maintenant
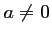 .
.
- a) Pour tout nombre
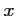 ,
,
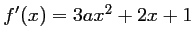 .
.
- b) Le discriminant du trinôme
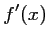 est
est
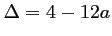 .
.
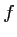 est croissante sur
est croissante sur
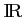 si et seulement si sa dérivée
si et seulement si sa dérivée 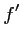 est toujours positive sur
est toujours positive sur
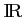 , et donc si et seulement si
, et donc si et seulement si
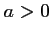 et
et
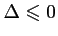 .
.
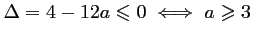 .
.
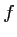 est donc croissante sur
est donc croissante sur
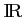 si et seulement si
si et seulement si
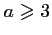 .
.
- a) Pour tout nombre
Cacher la correction
Voir aussi: