Exercice corrigé - ROC: formule de dérivation d'un carré et d'un cube
Applications
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - ROC: dérivée d'un produit, d'un carré et d'un cube. Applications
Exercice - énoncé:
ROC
Cacher la correction
Si ![]() et
et ![]() sont deux fonctions dérivables sur un intervalle
sont deux fonctions dérivables sur un intervalle ![]() ,
alors la fonction
,
alors la fonction ![]() est dérivable sur
est dérivable sur ![]() et
et
![]() .
.
- Démonstration
Démontrer que si
 est une fonction dérivable sur
est une fonction dérivable sur 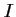 , alors:
, alors:
- a)
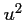 est dérivable sur
est dérivable sur 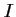 et
et
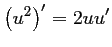 .
.
- b)
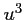 est dérivable sur
est dérivable sur 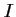 et
et
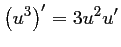 .
.
- a)
- Application
Justifier que les fonctions suivantes sont dérivables sur
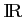 et
calculer l'expression de leurs dérivées.
et
calculer l'expression de leurs dérivées.
- a)
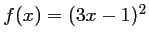
- b)
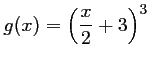 .
.
- a)
Correction exercice
- Démonstration
- a) D'après la propriété rappelée,
 est dérivable sur
est dérivable sur  avec
avec
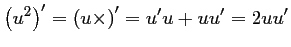 .
.
- b) de même,
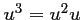 est dérivable sur
est dérivable sur  avec
avec
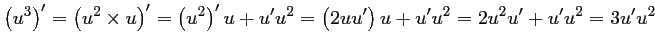
- a) D'après la propriété rappelée,
- Application
- a)
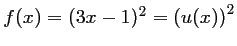 avec
avec 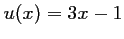 qui est une
fonction affine dérivable sur
qui est une
fonction affine dérivable sur
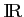 .
.
D'après la propriété du a),
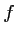 est donc dérivable sur
est donc dérivable sur
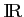 , avec
, avec
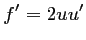 , soit
, soit
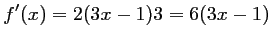 .
.
- b)
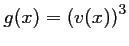 avec
avec
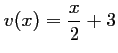 qui est une fonction
affine donc dérivable sur
qui est une fonction
affine donc dérivable sur
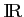 .
.
D'après la propriété du a),
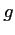 est donc aussi dérivable sur
est donc aussi dérivable sur
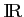 avec,
avec,
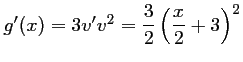
- a)
Cacher la correction
Voir aussi: