Exercices corrigés - Equations et inéquations du second degré
Résolution d'équations et inéquations
Première générale et scientifique
Exercice corrigé de mathématiques: Exercices corrigés - Résolution d'équations et inéquations du second degré
Exercice - énoncé:
Résoudre les équations ou inéquations :
Cacher la correction
- a)
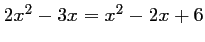
- b)
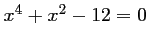
- c)
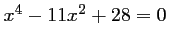
- d)
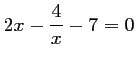
- e)
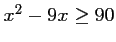
- f)
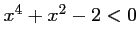
Correction exercice
- a)
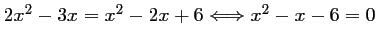 .
.
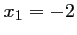 est solution, et comme
est solution, et comme 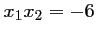 ,
, 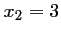 est aussi
solution, d'où
est aussi
solution, d'où
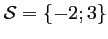 .
.
- b)
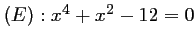 .
Soit
.
Soit 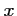 une solution éventuelle de
une solution éventuelle de 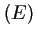 , et
, et 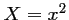 ,
alors
,
alors 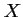 est solution de l'équation
est solution de l'équation
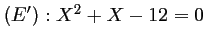 .
Cette équation admet pour solutions
.
Cette équation admet pour solutions 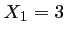 et
et 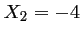 .
.
Ainsi, si
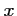 est une solution de (E), alors
est une solution de (E), alors 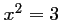 ou
ou 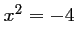 .
La première possibilité nous donne
.
La première possibilité nous donne
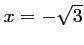 ou
ou
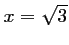 ,
tandis que la deuxième est impossible.
,
tandis que la deuxième est impossible.
Réciproquement, on vérifie bien que
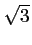 et
et 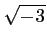 sont
solutions de (E), d'où
sont
solutions de (E), d'où
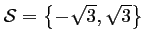 .
.
- c)
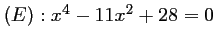 .
De même que précédemment, si
.
De même que précédemment, si 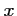 est solution de
est solution de 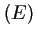 ,
on pose
,
on pose 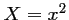 . Alors
. Alors 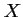 est solution de
est solution de
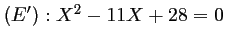 .
Cette équation du second degré a pour discriminant
.
Cette équation du second degré a pour discriminant 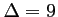 et
admet donc les deux solutions réelles distinctes:
et
admet donc les deux solutions réelles distinctes: 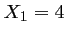 et
et
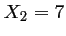 .
.
Ainsi, si
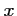 est solution de
est solution de 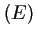 , alors
, alors 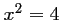 ou
ou 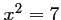 ,
d'où,
,
d'où, 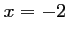 ou
ou 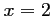 ou
ou
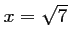 ou
ou
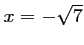 .
.
Réciproquement, on vérifie bien que ces valeurs sont solutions de
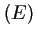 , et donc
, et donc
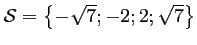 .
.
- d)
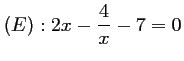 .
.
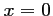 n'est pas solution de cette équation; on peut donc multiplier
chaque membre par
n'est pas solution de cette équation; on peut donc multiplier
chaque membre par 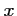 , et ainsi
, et ainsi
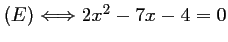 .
Cette équation du second degré a pour discriminant
.
Cette équation du second degré a pour discriminant 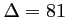 , et
donc pour solution
, et
donc pour solution
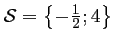 .
.
- e)
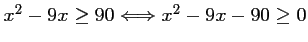 .
Le discriminant de ce trinôme est
.
Le discriminant de ce trinôme est
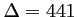 , et ses deux racines
sont
, et ses deux racines
sont 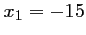 et
et 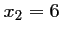 . Ce trinôme est donc positif ou nul pour
. Ce trinôme est donc positif ou nul pour
![$ x\in ]-\infty;-15] \cup [6;+\infty[$](/Generateur-Devoirs/1S/Chap1/ex1_c_img42.png) .
.
- f)
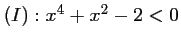 . Soit
. Soit 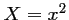 , alors
, alors 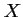 est solution de
est solution de
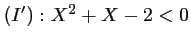 . Les deux racines de ce trinôme sont
. Les deux racines de ce trinôme sont
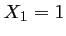 (racine évidente) et
(racine évidente) et 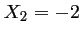 (car
(car 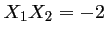 ).
).
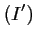 est donc vérifiée pour
est donc vérifiée pour 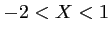 , soit
, soit 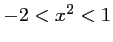 .
.
Pour tout
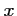 réel,
réel,
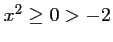 , tandis que
, tandis que
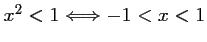 .
Finalement,
.
Finalement,
![$ \mathcal{S}=]-1;1[$](/Generateur-Devoirs/1S/Chap1/ex1_c_img53.png) .
.
Cacher la correction
Voir aussi: