Loi binomiale - Répétition d'expériences aléatoires

Loi binomiale

On s'intéresse précisément, comme dans les exercices précédents, à la probabilité d'obtenir un certain nombre de succès dans un schéma de Bernoulli.
Par exemple:

Lancer 10 fois successivement une pièce: quelle est la probabilité d'obtenir exactement 5 fois Pile ? ou de n'obtenir qu'une seule fois Pile ?
Tirer successivement, en les remettant ensuite dans le paquet, 4 cartes dans un jeu. Quelle est la probabilité de tirer successivement 4 as ? 2 as ?
Quelle est la probabilité d'avoir une fratrie de 4 enfants avec 3 garçons ?
Un test de dépistage a un taux d'erreur de 1%. Je fais 5 test successifs, quelle est la probabilité que 3 tests sur les 5 soient erronnés ?
Un QCM compte 10 questions, chacune comportant 4 réponses proposées. Quelle est la probabilité pour que je réponde juste à au moins 5 questions ?
Convoquer une assemblée ou toutes les personnes convoquées ne viennent qu'avec une certaine probabilité, indépendamment des autres. Quelle est la probabilité qu'au moins la moitité des personnes soient là ? les 3 quarts ?
...

Remarque sur l'utilisation d'arbres et leur complexité

On traîte à chaque fois un schéma de Bernoulli de paramètres n (répétitions) et p (probabilité du succès à chaque répétition).
En toute rigueur, peu importe les valeurs de ces paramètres, il suffit de réaliser un arbre pondéré comme dans les exercices précédents, et de calculer la probabilité en utilisant les règles de calcul sur les arbres pondérés, comme dans les exercices précédents.

À chaque répétition, l'arbre se divise en 2 branches: un succès et un échec, et ainsi,

pour 2 répétitions, l'arbre comporte 2 × 2 = 2² = 4 chemins,
pour 3 répétitions, l'arbre comporte 2 × 2 × = 2³ = 8 chemins,
pour 4 répétitions, l'arbre comporte de même 2⁴ = 16 chemins,
...
pour n répétitions, l'arbre comporte 2ⁿ chemins.

Déjà, le cas d'un arbre avec 16 ou 32 chemins n'est pas très attirant, ne serait-ce qu'à dessiner, même si on imagine encore pouvoir le faire si c'est vraiment nécessaire.
Pour un plus grand nombre, n = 10 répétitions par exemple, on obtient 2¹⁰ = 1024 chemins, et pour n = 20 répétitions on obtient 2²⁰ = 2¹⁰ ² ≈ 10⁶, soit plus de un million de chemins !

Clairement, l'utilisation d'arbres pondérés a ses limites.
Par contre, on peut néanmoins dégager une loi qui permet de d'effectuer ces calculs de probabilités: cette loi s'appelle la loi binomiale.

Variable aléatoire égale au nombre de succès

On reste dans le cadre précédent de schémas de Bernoulli de paramètres n et p : n répétitions d'une épreuve de Bernoulli dont le succès a pour probabilité p (et l'échec pour probabilité q = 1 − p).

On s'intéresse à la probabilité d'avoir un certain nombre de succès parmi ces répétitions (par exemple obtenir 3 six en lançant 10 fois un dé, ou répondre juste à 5 questions dans un QCM comportant 10 questions).
On note à cette fin X la variable aléatoire égale au nombre de succès, qui peut donc prendre les valeurs 0, 1, 2, ... , n.

Par exemple,

l'événement X = 2 désigne l'événement "obtenir 2 succès"
l'événement X ≥ 2 désigne l'événement "obtenir plus de 2 succès", ou encore "au moins 2 succès", c'est-à-dire en obtenir 2, ou 3, ou ..., ou n
l'événement X > 2 désigne l'événement "obtenir strictement plus de 2 succès", c'est-à-dire en obtenir 3, ou 4, ou ..., jusqu'à n
l'événement X ≤ 2 désigne l'événement "obtenir moins de 2 succès", c'est-à-dire en obtenir 0, 1 ou 2

Avec ces notations, on peut reprendre l'exercice 4 précédent:

Exercice 5

Lorsque j'appelle un ami pour jouer au tennis et qu'il me répond "oui, je viendrai jouer, c'est presque sûr", cela signifie qu'il y a 9 chances sur 10 pour qu'il vienne effectivement jouer.
Afin d'augmenter mes chances d'avoir un partenaire pour jouer, j'appelle 3 amis qui m'ont tous répondu: "oui, je viendrai jouer, c'est presque sûr".

On est en présence d'un schéma de Bernoulli, de paramètres n = 3 et p = 0,9.
On note X la variable aléatoire égale au nombre de succès, c'est-à-dire dans le contexte de l'énoncé, On note X est égale au nombre d'amis qui va venir effectivement.

Reprendre les questions et réponses de l'exercice 4 précédent, en notant correctement les événements et leur probabilité.

Quelle est la probabilité pour que j'ai, effectivement une personne, et une seule, avec qui jouer ?

L'événement "une seule personne" est aussi l'événement "X = 1" et sa probabilité
P(X = 1) = 0,207
Quelle est la probabilité pour que j'ai au moins une personne avec qui jouer ?

L'événement "au moins une personne" est aussi l'événement "X ≥ 1" et sa probabilité
P(X ≥ 1) = 0,001
Quelle est la probabilité pour qu'on puisse jouer en double (à 4 donc) ?

L'événement "les trois personnes" correspond à 3 succès, donc à l'événement "X = 3" et sa probabilité
P(X = 3) = 0,729

Compter le nombre de chemins menant aux succès

Pour calculer la probabilité d'obtenir un certain nombre k de succès lors de n répétitions d'une expérience, il faut connaître le nombre de façons d'obtenir ces k succès.

Coefficients binomiaux

Définition

On note n k , qui se lit "k parmi n", et s'appelle coefficient binomial, le nombre de façons d'obtenir k succès parmi n répétitions.
Sur l'arbre représentant les répétitions de l'expérience, un arbre à n "étages", le coefficient binomial n k compte le nombre de chemin avec k succès.

Pour un petit nombre de répétitions, il est facile de représenter l'arbre et de donner les valeurs de ces coefficients:

n = 1 répétition

$\psset{yunit=.5cm}\begin{pspicture}(0,-2)(2,2) \psline(1.5,-1)(0,0)(1.5,1)\rput[l](1.7,1){S}\rput[l](1.7,-1){E} \rput[l](2.5,1){1 succès} \rput[l](2.5,-1){0 succès} \end{pspicture}$

Il y a 1 chemin comportant k = 1 succès, donc 1 1 = 1 et 1 chemin comportant k = 0 succès, donc 1 0 = 1 .
n = 2 répétitions

$\psset{yunit=.6cm}\begin{pspicture}(-.5,-3)(5,3) \def\pp{}\def\pq{} \psline(1,-1.5)(-.3,0)(1,1.5)\rput(.3,1){\pp}\rput(.3,-1.1){\pq} \rput(1.2,-1.5){E}\rput(1.2,1.5){S} \psline(2.5,2.2)(1.5,1.5)(2.5,.8) \rput(1.9,2){\pp}\rput(1.9,.9){\pq} \rput(2.7,2.2){S}\rput(2.7,.8){E} \psline(2.5,-2.2)(1.5,-1.5)(2.5,-.8)\rput(1.9,-2.1){\pq}\rput(1.9,-1){\pp} \rput(2.7,-2.2){E}\rput(2.7,-.8){S} % \rput[l](3.5,2.2){2 succès} \rput[l](3.5,.8){1 succès} \rput[l](3.5,-.8){1 succès} \rput[l](3.5,-2.2){0 succès} \end{pspicture}$

Il y a 1 chemin comportant k = 2 succès, donc 2 2 = 1 , et 2 chemins comportant k = 1 succès, donc 2 1 = 2 , et enfin 1 seul chemin comportant k = 0 succès, 2 0 = 1 .
n = 3 répétitions

$\psset{yunit=.8cm}\begin{pspicture}(-.5,-3)(5,3) \def\pp{}\def\pq{} \psline(1,-1.5)(-.3,0)(1,1.5)\rput(.3,1){\pp}\rput(.3,-1.1){\pq} \rput(1.2,-1.5){E}\rput(1.2,1.5){S} \psline(2.5,2.2)(1.5,1.5)(2.5,.8) \rput(1.9,2){\pp}\rput(1.9,.9){\pq} \rput(2.7,2.2){S}\rput(2.7,.8){E} \psline(4,2.6)(3,2.2)(4,1.8) \rput(3.5,2.6){\pp}\rput(3.5,1.7){\pq} \rput(4.2,2.6){S}\rput(4.2,1.8){E} \psline(3,.8)(4,.4) \psline(4,1.2)(3,.8) \rput(3.5,1.2){\pp}\rput(3.5,.3){\pq} \rput(4.2,1.2){S}\rput(4.2,.4){E} \psline(2.5,-2.2)(1.5,-1.5)(2.5,-.8) \rput(1.9,-2.1){\pq}\rput(1.9,-1){\pp} \rput(2.7,-2.2){E}\rput(2.7,-.8){S} \psline(4,-1.2)(3,-.8)(4,-.4) \rput(3.5,-1.3){\pq}\rput(3.5,-.4){\pp} \rput(4.2,-1.2){E}\rput(4.2,-.4){S} \psline(4,-2.6)(3,-2.2)(4,-1.8) \rput(3.5,-2.7){\pq}\rput(3.5,-1.8){\pp} \rput(4.2,-2.6){E}\rput(4.2,-1.8){S} % \rput[l](5,2.6){3 succès} \rput[l](5,1.8){2 succès} \rput[l](5,1.2){2 succès} \rput[l](5,.4){1 succès} \rput[l](5,-.4){2 succès} \rput[l](5,-1.2){1 succès} \rput[l](5,-1.8){1 succès} \rput[l](5,-2.6){0 succès} \end{pspicture}$

Il y a 1 chemin comportant k = 3 succès, donc 3 3 = 1 , et 3 chemins comportant k = 2 succès, donc 3 2 = 3 puis 3 chemins comportant k = 1 succès donc 3 1 = 3 et enfin 1 seul chemin comportant k = 0 succès, donc 3 0 = 1
Cas général, n quelconque

$\begin{pspicture}(-.5,-4)(9,4) \def\pp{p}\def\pq{q} \psline(1,-1.5)(-.3,0)(1,1.5)\rput(.3,1){\pp}\rput(.3,-1.1){\pq} \rput(1.2,-1.5){E}\rput(1.2,1.5){S} \psline(2.5,2.2)(1.5,1.5)(2.5,.8) \rput(1.9,2){\pp}\rput(1.9,.9){\pq} \rput(2.7,2.2){S}\rput(2.7,.8){E} \psline(4,2.6)(3,2.2)(4,1.8) \rput(3.5,2.6){\pp}\rput(3.5,1.7){\pq} \rput(4.2,2.6){S}\rput(4.2,1.8){E} \psline(3,.8)(4,.4) \psline(4,1.2)(3,.8) \rput(3.5,1.2){\pp}\rput(3.5,.3){\pq} \rput(4.2,1.2){S}\rput(4.2,.4){E} \psline(2.5,-2.2)(1.5,-1.5)(2.5,-.8) \rput(1.9,-2.1){\pq}\rput(1.9,-1){\pp} \rput(2.7,-2.2){E}\rput(2.7,-.8){S} \psline(4,-1.2)(3,-.8)(4,-.4) \rput(3.5,-1.3){\pq}\rput(3.5,-.4){\pp} \rput(4.2,-1.2){E}\rput(4.2,-.4){S} \psline(4,-2.6)(3,-2.2)(4,-1.8) \rput(3.5,-2.7){\pq}\rput(3.5,-1.8){\pp} \rput(4.2,-2.6){E}\rput(4.2,-1.8){S} % \psline(5,2.4)(4.5,2.6)(5,2.8) \psline[linewidth=2pt,linestyle=dotted](5.2,2.9)(6.8,3.5)\rput[l](7.2,3.6){n succès} % \psline(5,1.6)(4.5,1.8)(5,2) \psline(5,1)(4.5,1.2)(5,1.4) \psline(5,.2)(4.5,.4)(5,.6) \psline(5,-.6)(4.5,-.4)(5,-.2) \psline(5,-1.4)(4.5,-1.2)(5,-1) \psline(5,-2)(4.5,-1.8)(5,-1.6) % \psline[linewidth=2pt,linestyle=dotted](6,.9)(6.8,.9) \psline[linewidth=2pt,linestyle=dotted](6,1.4)(6.8,.9) \psline[linewidth=2pt,linestyle=dotted](6,-.5)(6.8,.9) \rput[l](7.2,.9){k succès} \rput[l](7.2,.3){nombre de} \rput[l](7.2,-.1){chemins:} \rput[l](7.7,-1){$\dsp\binom{n}{k}$} \psline(5,-2.8)(4.5,-2.6)(5,-2.4) \psline[linewidth=2pt,linestyle=dotted](5.2,-2.9)(6.8,-3.5)\rput[l](7.2,-3.6){0 succès} \end{pspicture}$

On a toujours 1 seul chemin comportant k = n succès (que des succès, c'est le chemin du haut) et k = 0, donc n n = n 0 = 1

Les autres coefficients binomiaux sont plus difficiles à obtenir. Plusieurs manières permettent de les obtenir.

Triangle de Pascal

Le triangle de Pascal est très connu et utilisé en mathématiques. On le retrouve parfois dans des situations surprenantes (voir par exemple l'aspect fractal de ce triangle de Pascal dans lequel se dessine le triangle fractal de Sierpinski).
Le triangle de Pascal est le "triangle" de nombres dont les premières lignes sont:

$\begin{tabular}[t]{*6{p{0.41cm}}c} 1 &&&&&\\ 1 & 1 &&&&\\ 1 & 2 & 1 &&&\\ 1 & 3 & 3 & 1 &&\\ 1 & 4 & 6 & 4 & 1 &\\ 1 & 5 & 10 & 10 & 5 &1 \\ 1 & \multicolumn{4}{c}{\dots \ \ \ \dots}&\\ \rule[-.5cm]{0em}{.5cm} \psline[linewidth=1.6pt,linestyle=dotted](0,.2)(0,-.3) &&&&&& \psline[linewidth=1.6pt,linestyle=dotted](-.2,.6)(1,-.3) \end{tabular}$

Dans ce tableaux, la première colonne ainsi que la diagonale ne contiennent que des 1.
Ensuite, chaque autre nombre se calcule en ajoutant le nombre du dessus avec le nombre au-dessus à gauche.

$\rput(1.9,-2.5){\blue+} \psellipse[linecolor=blue,linewidth=2pt](1.9,-2.48)(0.72,0.35) \rput(3.6,-3.5){\red+} \psellipse[linecolor=red,linewidth=2pt](3.56,-3.48)(0.72,0.35) \psline(0,0)(1.17,-1) \begin{tabular}[t]{|c|*6{p{0.41cm}}c|}\hline \rule[-.3cm]{0em}{1.cm} \rput(-0.2,-.05){$n$} \rput(0.2,0.3){$k$} & 0 & 1 & 2 & 3 & 4 & 5 &\dots \,\, \\\hline \rule[0cm]{0em}{.6cm} \ 0 \, & 1 &&&&&&\\ 1 & 1 & 1 &&&&&\\ 2 & 1 & 2 & 1 &&&&\\ 3 & 1 & \textbf{\blue3} & 3 & 1 &&&\\ 4 & 1 & 4 & 6 & 4 & 1 &&\\ 5 & 1 & 5 & \text{\!\!10} & \textbf{\!\!\red10} & 5 &1 &\\ 6 & 1 & \multicolumn{4}{c}{\dots \ \ \ \dots}&&\\ \rule[-.5cm]{0em}{.5cm} \psline[linewidth=1.4pt,linestyle=dotted](0,.2)(0,-.3) &&&&&&& \\\hline \end{tabular}$

Enfin, et c'est ce qui nous intéresse particulièrement ici, à la n-ième ligne et la k-ième colonne de ce triangle se trouve justement le coefficient binomial $\dsp\binom{n}{k}$ .
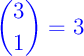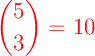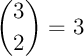On trouve par exemple dans ce tableau les valeurs $\blue\dsp\binom31=3$ , $\red\dsp\binom53=10$ , et aussi $\dsp\binom32=3$ , $\dsp\binom21=2$ , …

Avec la calculatrice

En utilisant le tableau de Pascal, on retrouve une difficulté similaire à celle rencontrée pour contruire l'arbre de probabilité pour un nombre n important de répétitions.
Ici, si le nombre

de répétitions est important, c'est le nombre de lignes qui est important. Or, il faut remplir toutes les lignes les unes après les autres pour pouvoir accéder à la n-ième ligne.

Les calculs de ces coefficients sont en général intégrés dans les calculatrices et autres logiciels permettant de faire des calculs mathématiques (tableur, python, ...).

Par exemple, à adapter éventuellement selon le modèle

Casio: dans le menu RUN, appuyer sur la touche OPTN, puis choisir PROB où on trouve enfin nCr.
Pour calculer par exemple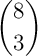 $\dsp\binom83$ , on tape d'abord 8 puis nCr puis 3
TI: avec la touche MATH on accède au menu PRB où on trouve nCr ou Combinaison (pour la version plus récente et française).
Pour calculer par exemple $\dsp\binom83$ , on tape d'abord 8 puis nCr puis 3
ou alors 8 puis Combinaison puis 3
Numworks: dans le catalogue Toolbox on accède au menu Dénombrement où on trouve binomial(n,k) qui permet de calculer la valeur du coefficient binomial correspondant.

Avec une formule de calcul explicite

On peut calculer les valeurs des coefficients binomiaux à l'aide du triangle de Pascal, voir ci-dessus, mais cette méthode est vite laborieuse. On peut aussi utiliser aveuglément la calculatrice, mais cela n'est pas toujours complètement satisfaisant.

On peut montrer la formule explicite

Propriété

On a la formule

$\binom{n}{k}=\dfrac{n!}{(n-k)!k!}$

où le point d'exclamation désigne le factoriel: le produit de l'entier concerné par tous les entiers inférieurs, soit

$n!=n\tm(n-1)\tm(n-2)\tm \dots \tm 2\tm1$

Par exemple

$3!=3\tm2\tm1=6$

ou encore

$6!=6\tm5\tm4\tm3\tm2\tm1=720$

On peut alors calculer directement les coefficients binomiaux souhaités, par exemple,

$\bgar{ll}\dsp\binom53&=\dfrac{5!}{(5-3)!3!}=\dfrac{5!}{2!\,3!}\\[1.2em] &=\dfrac{5\tm4\tm3\tm2\tm1}{2\tm1\,\tm\,3\tm2\tm1}\\[1em] &=10\enar$

Exercice 6

Calculer les coefficients binomiaux suivants (par la méthode de votre choix, voire bien sûr par les trois méthodes)
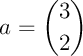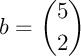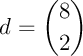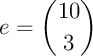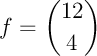
$a=\dsp\binom32$ ; $b=\dsp\binom52$ ; $c=\dsp\binom53$ ; $d=\dsp\binom82$ ; $e=\dsp\binom{10}3$ ; $f=\dsp\binom{12}4$

Loi binomiale

La loi binomiale est la loi de probabilité de la variable aléatoire égale au nombre de succès dans un schéma de Bernoulli.
Par exemple, pour un schéma de Bernoulli de paramètre

répétitions et une probabilité

du succès à chacune de ces répétitions, on a l'arbre suivant:

$\begin{pspicture}(-.5,-3)(5,3) \def\pp{p}\def\pq{q} \psline(1,-1.5)(-.3,0)(1,1.5)\rput(.3,1){\pp}\rput(.3,-1.1){\pq} \rput(1.2,-1.5){E}\rput(1.2,1.5){S} \psline(2.5,2.2)(1.5,1.5)(2.5,.8) \rput(1.9,2){\pp}\rput(1.9,.9){\pq} \rput(2.7,2.2){S}\rput(2.7,.8){E} \psline(4,2.6)(3,2.2)(4,1.8) \rput(3.5,2.6){\pp}\rput(3.5,1.7){\pq} \rput(4.2,2.6){S}\rput(4.2,1.8){E} \psline(3,.8)(4,.4) \psline(4,1.2)(3,.8) \rput(3.5,1.2){\pp}\rput(3.5,.3){\pq} \rput(4.2,1.2){S}\rput(4.2,.4){E} \psline(2.5,-2.2)(1.5,-1.5)(2.5,-.8) \rput(1.9,-2.1){\pq}\rput(1.9,-1){\pp} \rput(2.7,-2.2){E}\rput(2.7,-.8){S} \psline(4,-1.2)(3,-.8)(4,-.4) \rput(3.5,-1.3){\pq}\rput(3.5,-.4){\pp} \rput(4.2,-1.2){E}\rput(4.2,-.4){S} \psline(4,-2.6)(3,-2.2)(4,-1.8) \rput(3.5,-2.7){\pq}\rput(3.5,-1.8){\pp} \rput(4.2,-2.6){E}\rput(4.2,-1.8){S} \end{pspicture}$

et la probabilité de:

obtenir 3 succès: il y a un seul chemin avec 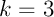succès, de probabilité 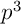, c'est-à-dire

$P(X=3)=p^3$
obtenir 2 succès: il y a un 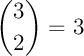$\dsp\binom32=3$ chemins avec 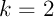succès, de probabilité chacun 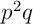, c'est-à-dire

$P(X=2)=\dsp\binom32p^2q=3p^2q$
obtenir 1 succès: il y a un $\dsp\binom31=3$ chemins avec succès, de probabilité chacun 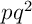, c'est-à-dire

$P(X=1)=\dsp\binom31pq^2=3pq^2$
obtenir 0 succès: il y a un seul chemin avec 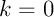succès, de probabilité 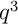, c'est-à-dire

$P(X=0)=q^3$

Exercice 7

On reprend l'exercice 3.
Un QCM est composé de 3 questions à chacune desquelles sont proposées 4 réponses. Une seule des réponses proposées est la bonne. Je décide de répondre au hasard à chaque question.
Quelle est la probabilité que je donne 3 bonnes réponses ? 2 bonnes réponses ? 1 seule ? aucune ?

Plus généralement, pour une expérience contenant un nombre quelconque de répétitions:

Théorème

Dans le cadre d'un schéma de Bernoulli de paramètres n répétitions, p la probabilité du succès à chaque répétition, et q = 1 − p celle de l'échec. On note X la variable aléatoire égale au nombre de succès lors de ces n répétitions.
Alors X suit la loi binomiale de paramètres n et p, notée ℬ(n ; p) et on a la probabilité d'obtenir k succès:

$P(X=k)=\binom{n}{k}p^kq^{n-k}$

L'espérance et l'écart type de la variable aléatoire X sont de plus donnés par:

E(X) = np σ(X) = npq

Exercice / exemple

Je lance 10 fois de suite une pièce bien équilibrée. Quelle est la probabilité que j'obtienne 7 fois Pile ?

Calculs pour la loi binomiale avec la calculatrice

La loi binomiale est une loi fondamentale en statistiques et probabilités. Les calculatrices (et logiciels de calcul, tableur, python, ...) permettent de calculer directement les valeurs des probabilités associées.
Elles donnent en fait, en générale, deux types de résultats:

la probabilité d'obtenir k succès, soit P(X = k).

Dans les Casio, dans STAT puis DIST (pour distribution) puis BINM (pour binomiale) et Bpd, et enfin un menu permet de saisir les paramètres.

Pour les TI, 2nd + DISTR ou 2nd + distrib puis binompdf et enfin compléter avec les paramètres voulus: binompdf(n,p,k).
la probabilité d'obtenir moins de k succès, soit P(X ≤ k).
On parle ici de probabilité cumulées, car
P(X ≤ k) = P(X = 0) + P(X = 1) + … + P(X = k)
et on cumule ainsi toutes les valeurs des probabilités de 0 à k.

Dans les Casio, comme précédemment, mais en choisissant finalement Bcd.
Pour les TI, comme précédemment aussi, mais en choisissant finalement binomcdf.

Voir aussi par exemple la calculette en ligne.

Exercice 8

On reprend l'exercice précédent sur les 10 lancers successifs d'une pièce bien équilibrée.
Quelle est la probabilité que j'obtienne, sur ces 10 lancers, moins de 6 Pile ?
Quelle est la probabilité que j'obtienne, sur ces 10 lancers, plus de 7 Pile ?